
1. Introduction
Adversarial learning methods의 가장 큰 문제점은 학습과정이 불안정하다는 것이다. 학습의 안정성을 위해서는 generator와 discriminator 사이의 학습 균형을 잘 유지하는 것이 아주 중요하다. Discriminator의 성능이 너무 좋으면 generator의 학습에 유용한 gradient가 잘 발생하지 않고, 그렇다고 discriminator의 성능이 나쁘면 generator가 학습하는 것을 방해하기 때문이다.
본 논문에서는 information bottleneck 역할을 하는 variation approximation을 사용하여 discriminator의 성능을 적절하게 유지하는 방안에 대해 다룬다. 저자들은 이 adaptive stochastic regularization method를 Variational Discriminator Bottleneck (VDB)라 명명하고, 이것이 imitation tasks, learning dynamic continuous control from video demonstrations, inverse reinforcement learning과 같이 여러가지 영역에서 폭넓게 사용되어 좋은 성능을 낼 수 있음을 보인다.
2. Preliminaries
본격적인 내용에 들어가기에 앞서 supervised learning 관점의 variational information bottleneck에 대해 알아보도록 하자. Feature \(x_i\), labels \(y_i\)로 이루어진 dataset \(\{x_i, y_i\}\)이 주어졌을때, 적절한 discriminator를 얻는 것은 다음 문제에 대한 solution \(q^*(y_i \mid x_i)\)를 찾는 것과 같다.
\[\min_q \mathbb{E}_{x, y \sim p(x,y)} [-\log q(y|x)]\]하지만 위 문제는 푸는 과정에서 쉽게 overfitting을 야기하여 model이 data의 특이한 부분(idiosyncrasy)을 결과물에 반영하는 경우가 종종 생긴다. 이에 Alemi et al. (2016)는 information bottleneck이라는, mutual information을 이용한 regularization 기법을 제안했다.
\[\begin{align*} J(q, E) = \min_{q, E} \mathbb{E}_{x, y \sim p(x,y)} \big[ \mathbb{E}_{z \sim E(z|x)} [- \log q(y|z)] \big]\\ \text{s.t. } I(X,Z) \le I_c. \end{align*}\]3. Variational Discriminator Bottleneck
\(E(z \mid x)\)는 feature \(x\)를 latent distribution에 매핑(mapping)하는 encoder이며, \(I(X,Z)\)는 encoding된 feature와 original feature 간의 mutual information이다. 위 최적화 문제는 model이 가장 특징적인 feature를 중점적으로 보도록 하는 것이라고 볼 수 있다.
여기서 mutual information \(I(X, Z)\)를 좀 더 자세히 살펴보자. Mutual information이란 하나의 확률변수를 관측했을때 또 다른 확률변수에서 얻을 수 있는 정보량을 뜻한다. Mutual information의 정의에 의하면 \(I(X, Z)\)는 다음과 같이 전개된다.
\[\begin{align*} I(X,Z) &= \int p(x,z) \log \frac{p(x,z)}{p(x)p(z)} dxdz\\ &= \int p(x) \frac{p(x,z)}{p(x)} \log \frac{p(x,z)}{p(x)p(z)} dxdz\\ &=\int p(x) E(z|x) \log \frac{E(z|x)}{p(z)} dx dz\\ \end{align*}\]Mutual information을 계산하기 위해서는 marginal distribution \(p(z) = \int E(z \mid x) p(x) dx\)을 계산해야 하는데, 이것을 계산하는 것이 intractable하므로 variational lower bound를 사용하여 문제의 contraint를 약간 변형한다.
우선 marginal에 대한 근사함수 \(r(z)\)을 도입해보겠다. 항상 참인 명제 \(KL[p(z) \| r(z)] \ge 0\)로부터 \(p(z)\)와 \(r(z)\)의 관계식을 유도해보자.
\[\begin{align*} KL[p(z) \| r(z)] &= \int p(z) \log \frac{p(z)}{r(z)} dz\\ &= \int p(z) \log p(z) dz - \int p(z) \log r(z) dz\\ &\ge 0\\\\ \Leftrightarrow \int p(z) \log p(z) dz &\ge \int p(z) \log r(z) dz\\ \end{align*}\]이 관계를 이용하면 \(I(X,Z)\)의 upper bound를 구할 수 있다.
\[\begin{align*} I(X,Z) &= \int p(x) E(z|x) \log \frac{E(z|x)}{p(z)} dx dz\\ &\le \int p(x) E(z|x) \log \frac{E(z|x)}{r(z)} dx dz\\ &= \mathbb{E}_{x \sim p(x)} \big[ KL[E(z|x) \| r(z)] \big]. \end{align*}\]\(I(X,Z)\)의 upper bound를 활용하여 앞서 정의한 문제 \(J(q, E)\)에 대한 tractable upper bound인 \(\tilde{J}(q, E)\)를 정의해보자. (\(\tilde{J}(q, E) \ge J(q, E)\))
\[\begin{align*} \tilde{J}(q, E) = \min_{q, E} \mathbb{E}_{x, y \sim p(x,y)} \big[ \mathbb{E}_{z \sim E(z|x)} [- \log q(y|z)] \big]\\ \text{s.t. } \mathbb{E}_{x \sim p(x)} \big[ KL[E(z|x) \| r(z)] \big] \le I_c. \end{align*}\]Unconstrained optimization으로 위 문제에 접근한다면 문제를 Lagrangian형태로 변형하여 unconstrained problem으로 변환할 수 있다. (with coefficient \(\beta\))
\[\min_{q, E} \mathbb{E}_{x, y \sim p(x,y)} \big[ \mathbb{E}_{z \sim E(z|x)} [- \log q(y|z)] \big] + \beta \big( \mathbb{E}_{x \sim p(x)} \big[ KL[E(z|x) \| r(z)] \big] - I_c \big).\]Variational Information Bottleneck (VIB)은 overfitting을 줄이는 효과가 있으며 도한 adversarial examples에 대해 robust한 특성을 보인다.
4. Variational Discriminator Bottleneck
다음은 discriminator \(D\)와 generator \(G\)로 구성되어있는 기본적인 GAN framework다.
\[\max_G \min_D \mathbb{E}_{x \sim p^*(x)} [ -\log(D(x))] + \mathbb{E}_{x \sim G(x)} [-\log(1-D(x))].\]Discriminator에 encoder \(E(z \mid x)\)를 도입하여 GAN’s discriminator + VIB의 문제를 정의해보자.
\[\begin{align*} J(D, E) = \min_{D, E} \mathbb{E}_{x \sim p^*(x)} \big[ \mathbb{E}_{z \sim E(z|x)} [ -\log(D(z))] \big] + \mathbb{E}_{x \sim G(x)} \big[ \mathbb{E}_{z \sim E(z|x)}[-\log(1-D(z))] \big]\\ \text{s.t. } \mathbb{E}_{x \sim \tilde{p}(x)} \big[ KL[E(z|x) \| r(z)] \big] \le I_c,\\ \text{with } \tilde{p} = \frac{1}{2}p^* + \frac{1}{2}G \text{ being a mixture of the target distribution and the generator.} \end{align*}\](mixture distribution은 (특히 초반의) 학습이 잘 되지 않은 \(G\)에 의해 일어날 수 있는 high variance를 방지한다.)
위의 문제를 Variational Discriminator Bottleneck (VDB)라 명명한다. 또한 Lagrange function을 통해 동일한 문제를 아래와 같이도 정의할 수 있다. (\(\beta\) is a Lagrangian multiplier)
\[\begin{align*} J(D, E) &= \min_{D, E} \max_{\beta \ge 0} \mathbb{E}_{x \sim p^*(x)} \big[ \mathbb{E}_{z \sim E(z|x)} [ -\log(D(z))] \big] + \mathbb{E}_{x \sim G(x)} \big[ \mathbb{E}_{z \sim E(z|x)}[-\log(1-D(z))] \big]\\ &+ \beta \big( \mathbb{E}_{x \sim \tilde{p}(x)} \big[ KL[E(z|x) \| r(z)] \big] - I_c \big)\\\\ &= \min_{D, E} \max_{\beta} L(D, E, \beta) \end{align*}\]Dual Gradient Method를 통해 위 문제를 푼다면 \(D, E, \beta\)에 대한 update는 아래의 과정을 반복하게 될 것이다.
\[\begin{align*} D, E &\leftarrow arg\min_{D,E} L(D, E, \beta)\\ \beta &\leftarrow max \big(0, \beta + \alpha_\beta ( \mathbb{E}_{x \sim \tilde{p}(x)} \big[ KL[E(z|x) \| r(z)] \big] - I_c ) \big),\\\\ \text{where } \alpha_\beta &\text{ is a stepsize for the dual variable for dual gradient descent.} \end{align*}\]그 외
-
논문의 실험에서는 \(r\)을 정규분포로 설정한다. (\(r(z) = N(0, I)\))
-
Encoder는 mean \(\mu_E\), diagonal covariance matrix \(\Sigma_E(x)\)의 정규분포로 정의한다. \(E(z|x) = N(\mu_E(x), \Sigma_E(x)\)
-
Generator의 목적함수에는 \(Z\)에 대한 expectation이 아니라 \(\mu_E(x)\)를 이용한 근사식을 사용하여 실험에서 충분한 성능을 냈다.
- Discriminator는 sigmoid를 activation으로 사용하는 single linear unit으로 모델링되었다.
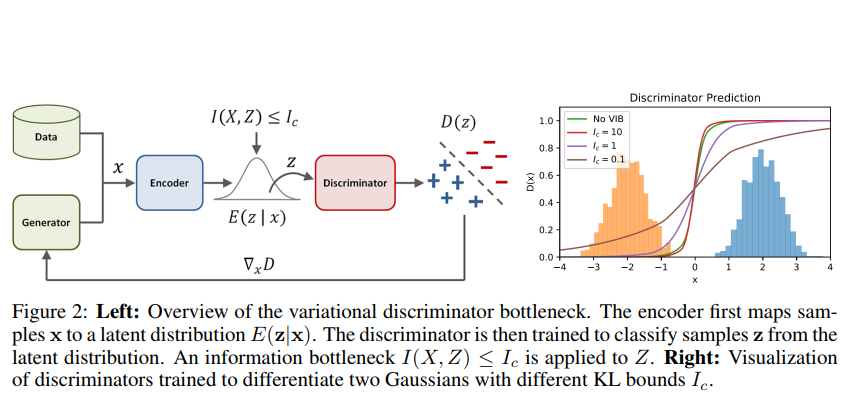
Fig2의 우측 그림은 disjoint support의 2개 가우시안 분포에 대한 discriminator의 decision boundary를 가시화한 것이다. Constraint가 느슨해질수록 decision boundary가 더 날카로워지는 것을 확인할 수 있다. 즉, \(I_c\)가 낮아질수록 decision boundary가 완만해지므로, generator의 학습을 위한 informative gradient가 더욱 제공될 것이다.
5. VAIL: Variational Adversarial Imitating Learning
Ho & Ermon (2016)은 generative adversarial imitation learning (GAIL)을 통해 target policy \(\pi^*(s)\)와 agent의 policy \(\pi(s)\)로부터의 state distributions를 구분하는 discriminator를 제안했다.
\[\max_\pi \min_D \mathbb{E}_{s \sim \pi^*(s)} [ -\log(D(s)) ] + \mathbb{E}_{s \sim \pi(s)} [-\log(1 - D(s))].\]VDB를 discriminator에 도입하면 최적화 문제는 아래와 같이 변형되고, 저자들은 이를 Variational Adversarial Imitation Learning (VAIL)이라 칭한다.
\[\begin{align*} J(D, E) &= \min_{D, E} \max_{\beta \ge 0} \mathbb{E}_{x \sim \pi^*(x)} \big[ \mathbb{E}_{z \sim E(z|x)} [ -\log(D(z))] \big] + \mathbb{E}_{x \sim \pi(x)} \big[ \mathbb{E}_{z \sim E(z|x)}[-\log(1-D(z))] \big]\\ &+ \beta \big( \mathbb{E}_{x \sim \tilde{\pi}(x)} \big[ KL[E(z|x) \| r(z)] \big] - I_c \big)\\\\ \text{where } &\tilde{\pi} = \frac{1}{2}\pi^* + \frac{1}{2}\pi \text{ represents a mixture of the target policy and the agent's policy.} \end{align*}\]6. VAIRL: Variational Adversarial Inverse Reinforcement Learning
Fu et al. (2017)는 Adversarial Inverse Reinforcement Learning (AIRL)을 통해 disentangled reward function을 학습하는 discriminator를 다음과 같이 정의했다.
\[D(s, a, s') = \frac{\exp(f(s,a,s'))}{\exp(f(s,a,s')) + \pi(a|s)},\\ \text{where } f(s,a,s') = g(s,a) + \gamma h(s') - h(s), \text{ with} g \text{ and } h \text{ being learned functions.}\]VAIRL에서는 stochastic encoders \(E_g(z_g\mid s), E_h(z_h\mid s), g(z_g), h(z_h)\)와 latent variable에 대한 함수 \(g(z_g), h(z_h)\)를 도입되며 discriminator는 아래와 같이 변형된다.
\[D(s, a, z) = \frac{\exp(f(z_g,z_h,z_h'))}{\exp(f(z_g,z_h,z_h')) + \pi(a|s)},\\ \text{for } z=(z_g, z_h, z_h') \text{ and } f(z_g, z_h, z_h') = D_g(z_g) + \gamma D_h(z_h') - D_h(z_h).\]또한 VAIRL의 최적화 문제는 아래와 같다.
\[\begin{align*} J(D, E) = \min_{D, E} \max_{\beta \ge 0} \mathbb{E}_{s,s' \sim \pi^*(s,s')} \big[ \mathbb{E}_{z \sim E(z|s,s')} [ -\log(D(s,a,z))] \big]\\ + \mathbb{E}_{s,s' \sim \pi(s,s')} \big[ \mathbb{E}_{z \sim E(z|s,s')}[-\log(1-D(s,a,z))] \big]\\ + \beta \big( \mathbb{E}_{s,s' \sim \tilde{\pi}(s,s')} \big[ KL[E(z|s,s') \| r(z)] \big] - I_c \big)\\\\ \text{where } \pi(s, s') \text{ denotes the joint distribution of successive state from a policy,}\\ \text{and } E(z|s,s') = E_g(z_g|s)\cdot E_h(z_h|s) \cdot E_h(z_h'|s'). \end{align*}\]7. Experiments
VDB가 imitation learning, inverse reinforcement learning, image generation에 대해 효과적으로 작동하는지 실험해본다.
7.1 VAIL: Variational Adversarial Imitating Learning
Mocap clip의 single demonstration을 얼마나 잘 따라하는지 측정하는 실험이다. 128차원의 encoding \(Z\), information constraint \(I_c = 0.5\), dual stepsize \(\alpha_\beta = 10^{-5}\)를 사용하였으며, policy의 학습에는 PPO를 이용했다.
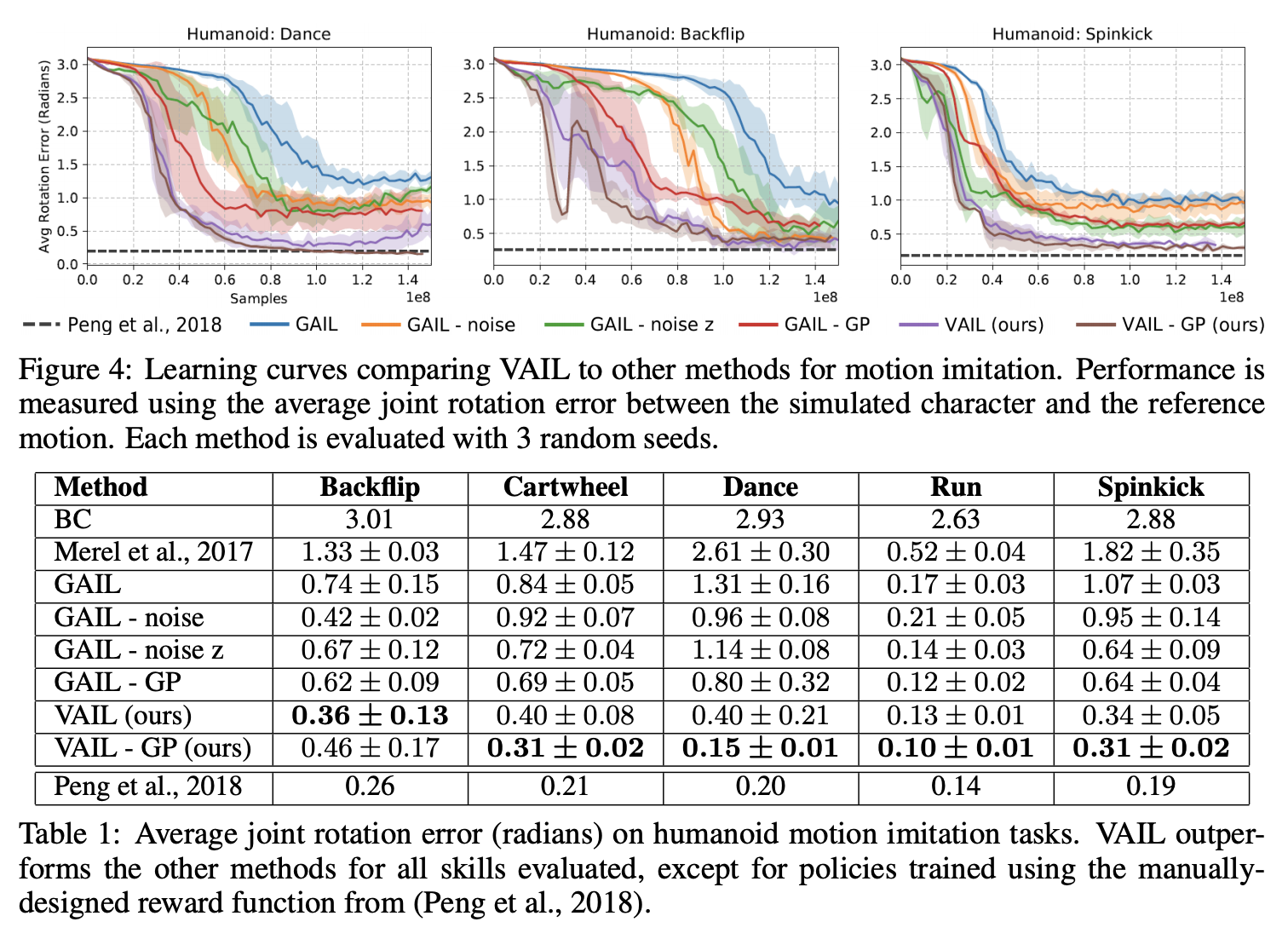
VAIL과 VAIL-GP (Gradient Penalty to the discriminator)가 가장 좋은 성능을 보였으며, handcrafted reward를 사용한 경우에 전반적으로 상당히 근접한 결과를 얻어냈다.
7.2 VAIRL: Variational Adversarial Inverse Reinforcement Learning
C-Maze와 S-Maze 환경에서 dynamics의 변동이 발생하더라도 agent의 유의미한 behaviour를 얼마나 잘 유지하는지 측정해보았다. C-Maze에서 AIRL이 gradient penalty 없이는 overfitting으로 인해 transferring에 실패하는 모습을 종종 보인 반면에, VAIRL은 gradient penalty 없이도 transferring task에 좀 더 안정적인 모습을 보였다. 또한 KL constraint를 사용하지 않았을때 두 개의 task에서 VAIRL의 성능이 떨어지는 것을 관찰할 수 있었다.

7.3 VGAN: Variational Generative Adversarial Networks
VDB를 이미지 생성모델에 적용하여 CIFAR-10, CelebA, CelebAHQ 데이터셋을 이용해 실험해보았다. 실험 비교군은 근래 제안되었던 stabilization technicques인 WGAN-GP, Spectral Normalization (SN), Gradient Penalty (GP) 및 original GAN이 채택되었다. 성능 측정에는 Fréchet Inception Distance (FID)를 이용하였다.
모든 methods는 Mescheder et al. (2018)의 resnet architecture를 base model로 구현하였고, VGAN의 경우 KL constraint \(I_c\)외의 모든 파라미터는 Mescheder et al. (2018)의 것을 그대로 사용했다.
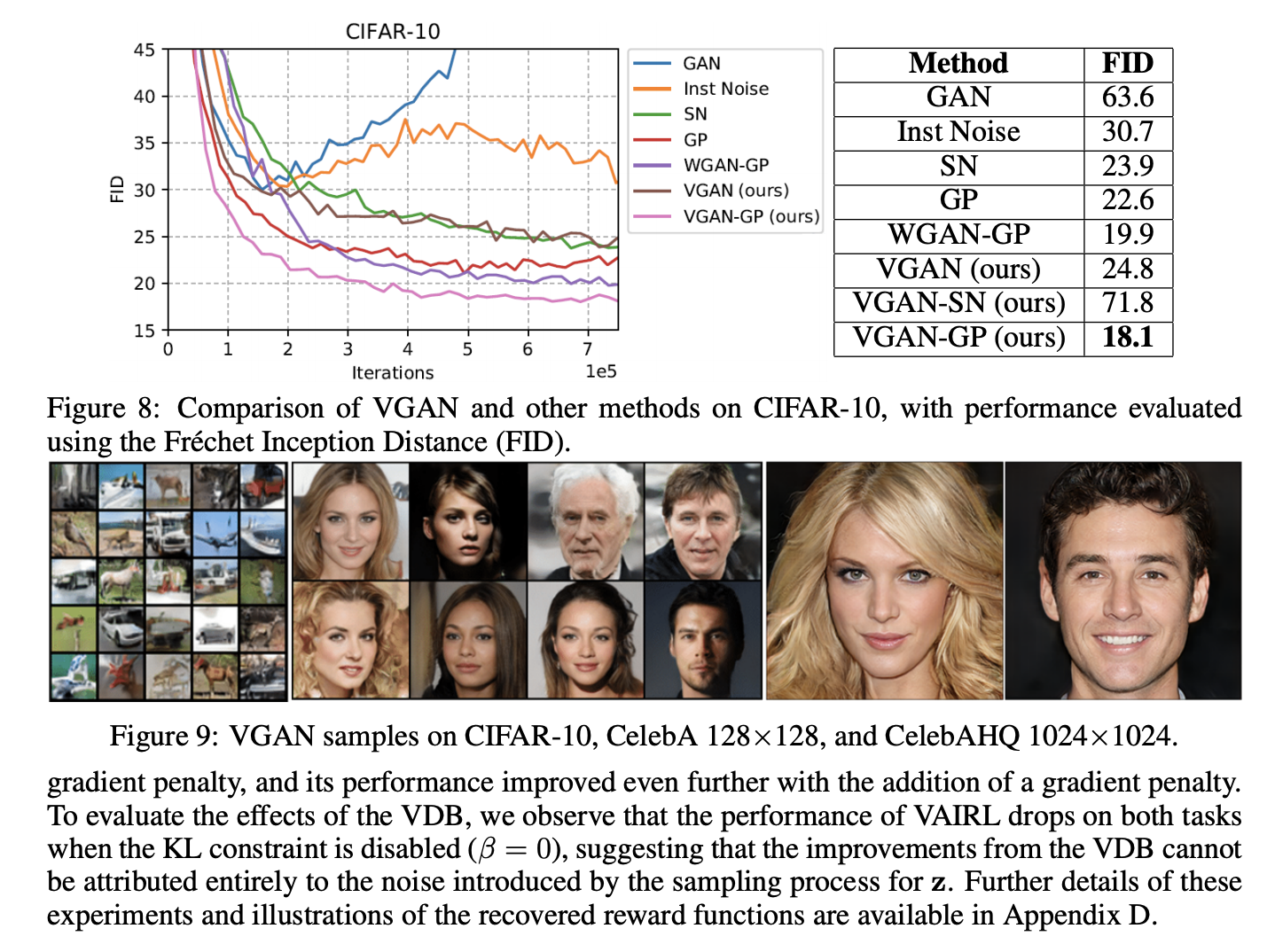
VDB에 Gradient Penalty가 적용된 것이 가장 좋은 성능을 보였으며, VDB에 SN이 적용된 경우에는 쉽게 diverging하는 모습이 관찰되었다.