
1. 문제상황 및 목표
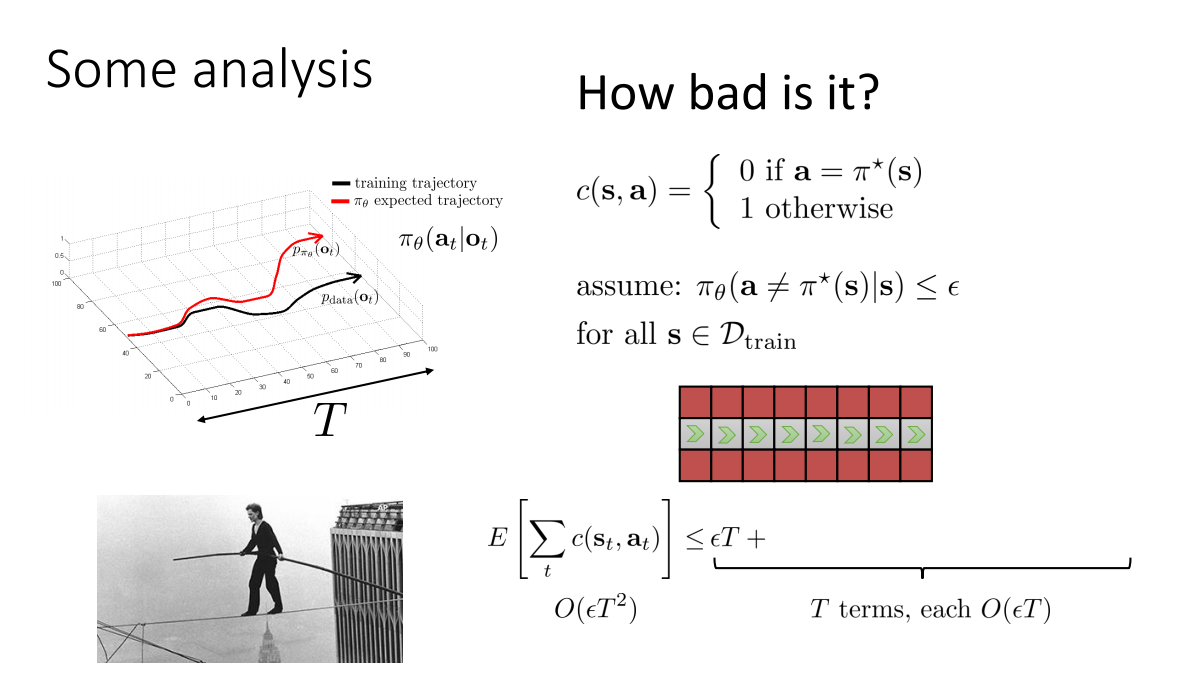
Imitation learning에서 supervised learning으로의 접근은 좋은 효과를 발휘하기도 하지만, long-range & goal-directed behaviour에 대해서는 적용이 어렵다는 것이 증명되어있다. 발생할 수 있는 오차는 아래와 같이 \(O(\epsilon T^2)\)로 계산된다 (cs294-112 lecture2: Supervised Learning and Imitation (2018)).
이에 대해 일각에서는 long-horizon goal-directed behaviour에 대해 perception subsystem과 planning subsystem을 통해 접근하려는 동향을 보이고 있다. Perception system은 환경을 다양한 모델과 feature로 계산해내는 역할을 하고, planning은 입력받은 cost map을 바탕으로 long-horizon에 대한 minimal risk (cost) path를 계산하는 역할을 한다. 문제는 planning을 위해 perception model을 cost로 연결시키는 것이 매우 어렵고, 이것이 종종 hand-designed heuristic에 의존적이라는 것이다.
이 연구의 목표는 feature에서 cost function으로의 mapping을 학습시킴으로써 cost function으로 도출된 Markov Decision Problem의 optimal policy가 expert’s behaviour를 모방하게 하는 것에 있다.
2. 주요한 공헌
이 연구의 주요한 공헌은 다음 세 가지로 요약할 수 있다.
- Learning to plan을 위한 새로운 방법론을 제안
- 구조화된 maximum-margin classification에 대한 효과적이고, 간단한 접근법을 제시
- Mobile robotics와 연관된 문제들에 본 방법론이 실제적으로 적용가능함을 보임
3. 문제정의 (Problem Formulation)
Structured large margin criteria는 다음의 QP문제를 푸는 것으로 생각할 수 있다.
\[\begin{align*} \min_{\omega, \zeta_i} \frac{1}{2} \| \omega \|^2 + \frac{\gamma}{n} \sum_i \beta_i \zeta_i^q\\ \text{s.t } \: \forall i, \: \omega^T f_i(y_i) + \zeta_i \ge \max_{\mu \in \mathcal{G}_i} \omega^T F_i \mu + l_i^T \mu\\ \end{align*}\]여기서 inequality constraint의 우항을 dual form으로 변경하고, 이때의 dual variable \(v\)가 Bellman primal constraints를 만족한다고 하면 이는 다음의 one compact quadratic problem으로 변환된다.
\[\begin{align*} \min_{\omega, \zeta_i} \frac{1}{2} \| \omega \|^2 + \frac{\gamma}{n} \sum_i \beta_i \zeta_i^q\\ \text{s.t } \: \forall i \quad \omega^T f_i(y_i) + \zeta_i \ge s_i^Tv_i\\ \forall i, x, a \quad v_i^x \ge (\omega^T F_i + l_i)^{x,a} + \sum_{x'} p_i(x' | x,a) v_i^{x'}\\ \end{align*}\]4. 최적화
하지만 3에서 도출한 quadratic programming은 풀기에 다소 복잡도가 높을 수 있다. 여기서는 MDP의 특정 class에 대해 더 빠르게 동작하는 것으로 알려진 policy iteration이나 A*에 적합한 형태로 문제를 변경해보도록 할 것이다. 3의 서두에 제시된 문제를 hinge-loss form의 unconstrained optimization problem으로 재정의하겠다. 만약 slack variable \(\zeta_i\)가 충분히 작다고 한다면 inequality constraint에 의해 \(\zeta_i\)를 \(\max_{\mu \in \mathcal{G}_i} (\omega^T F_i + l_i^T)\mu - \omega^T F_i \mu_i\)로 봐도 무방할 것이다. 이를 목적함수에 대입하면 다음의 새로운 목적함수를 유도할 수 있다.
\[c_q(\omega) = \frac{1}{n} \sum_{i=1}^{n} \beta_i \big( \max_{\mu \in \mathcal{G}_i} (\omega^T F_i + l_i^T)\mu - \omega^T F_i \mu_i \big)^q + \frac{\lambda}{2} \| \omega \|^2\]그리고 위 문제의 subgradient는 (subgradient의 기본성질에 의해) 다음과 같이 유도된다.
\[g_{\omega}^{q} = \frac{1}{n} \sum_{i=1}^{n} q\beta_i \big((\omega^T F_i)\mu^* - \omega^T F_i \mu_i \big)^{q-1} \cdot F_i \Delta^\omega \mu_i + \lambda \omega\]논문에서는 위 subgradient \(g_{\omega}^{q}\)를 이용하여 최적화를 시행한다. (Note: subgradient는 descent를 보장하지 않기때문에 optional하게 additional constraint로 \(\omega\)를 projection 할 수 있다.)
논문의 3.1에서는 objective function이 strong convexity를 만족할때, 충분히 작은 constant stepsize에 대해 linear convergence rate를 보이며, diminishing stepsize (\(\alpha_t = \frac{r}{t} \: for \: t \ge 1\))에 대해서는 sublinear rate를 보임을 증명한다.
5. 실험
학습된 reward function을 A*알고리즘의 heuristic function으로 사용하여 path planning 문제에 대한 실험결과를 보인다. 이미지의 각 픽셀들에 대해 좌우, 대각선 8방향의 인접셀로 이동 가능한 것으로 문제를 설정한다. 또한 admissable heuristic function이 존재함을 가정하고 제약조건 \(F_i \ge 0\) (element-wise)을 추가한다. 매 iteration에서 projection을 통해 이 제약조건을 적용할 수 있다.
실험을 통해 optimal path가 아닌 경우라도 최종적으로 goal에 잘 도달하는 모습을 보인다 (Figure 2). 그리고 state의 특정 feature와 상응하는 weight에 대해 제약조건을 거는 것으로 prior knowledge를 주입하는 것이 가능함을 보인다 (Figure 1).