1. 문제정의 및 목적
주어진 demonstrator의 behaviour가 suboptimal(imperfect and noisy)일 경우, 이를 단 하나의 reward function으로 표현하는 것에 어려움이 생긴다 (ambiguity). 본 연구의 취지는 feature matching을 constraint로 두고 policy에 대한 entropy를 최대화시킴으로써 feature matching 알고리즘의 성능을 보장하면서도 well-defined, globally normalised distribution over decision sequences를 찾자는 것이다. (참고: cs294-112 lecture16-IRL)

2. Deterministic Path Distributions
Ambiguity 문제를 해결하기 위해 적절한 확률분포함수를 정의하고 이에 대해 maximum entropy를 취하도록 할 것이다. 확률분포함수 \(P(\zeta_i \mid \theta)\)를 다음과 같이 정의한다. (trajectory or path \(\zeta\), state \(s_i\), actions \(a_i\))
\[P(\zeta_i | \theta) = \frac{1}{Z(\theta)} e^{\theta^T f_{\zeta_i}} = \frac{1}{Z(\theta)} e^{\sum_{s_j \in \zeta_i} \theta^T f_{s_j}}\]\(\theta\)를 reward weights라고 할때, reward가 높을수록 해당 plan에 대한 선호도가 지수적으로 증가하는 형태라고 볼 수 있다. 여기서 \(Z(\theta)\)는 partition function으로, 확률분포함수의 그래프 아랫쪽 영역의 합이 1이 되도록 해준다. Partition function은 infinite horizon problem 또는 discounted reward weights의 infinite horizon problem에 대해 항상 수렴한다.
3. Non-Deterministic Path Distributions
일반적인 MDP 문제에서는 action은 state 간의 non-deterministic transition을 야기한다 (Figure1-(d) 참고). 이때의 state transition distribution을 \(T\)라고 하자. 또한 action outcome에 대한 space를 \(\tau\), 각 action에 대한 next state를 outcome sample \(o\), \(\zeta\)가 \(o\)와 compatible할때는 1, 나머지 경우에는 0을 반환하는 indicator function을 \(I_{\zeta \in o}\)라고 하자. 이때의 확률분포함수 \(P(\zeta_i \mid \theta, T)\)는 다음과 같다.
\[P(\zeta | \theta, T) = \sum_{o \in \tau} P_T(o) \frac{e^{\theta^T f_{\zeta}}}{Z(\theta, o)} I_{\zeta \in o}\]문제는 이 분포함수를 계산하는 것이 보통은 intractable하다는 것이다. 다음의 두 가지 가정 아래에 분포함수를 계산 가능한 형태로 변형한다.
-
Transition randomness가 behaviour에 대한 영향도가 아주 작다.
-
Partition function이 모든 \(o \in \tau\)에 대해 항상 같은 값을 가진다.
4. Learning from Demonstration
3에서 유도한 분포에 대해 maximum entropy를 취해줌과 동시에 관찰된 데이터에 대해 likelihood를 최대화 할 것이다.
\[\theta^* = argmax_{\theta} \sum_{examples} \log P(\tilde{\zeta} | \theta, T)\]위 문제의 목적함수는 concave이므로 gradient-based optimization을 통해 해결 가능하다. 즉, \(log P\)에 대해 전개한 식을 \(\theta\)에 대해 미분하고 이를 0으로 만드는 지점이 \(\sum_{examples} \log P(\tilde{\zeta} \mid \theta, T)\)가 최대화되는 위치인 것이다.
\[\nabla L(\theta) = \tilde{f} - \sum_{\zeta} P(\zeta | \theta, T) f_{\zeta} = \tilde{f} - \sum_{s_i} D_{s_i} f_{s_i} = 0\]이는 empirical feature count와 learner’s feature count간의 차이를 최소화시키는 것이라고도 볼 수 있다. (\(D\)는 state visitation frequencies)
위 문제의 변형과정은 cs294-112 lecture16-IRL에서 좀 더 자세히 설명된다. 아래 그림 맨 아래 수식의 두 번째 term이 soft optimal policy임을 유의깊게 보자.

5. Efficient State Frequency Calculations
State frequency \(D\)를 계산하는 알고리즘을 소개한다.

6. 실험
주행경로 예측문제에 본 알고리즘을 적용한다.
- 택시에 대한 GPS데이터로부터 구간이 짧거나 noisy한 정보를 제거하는 등 전처리
- 각 도로 segment에 대해 road type, speed, lanes, transitions 4가지 타입의 feature를 부여
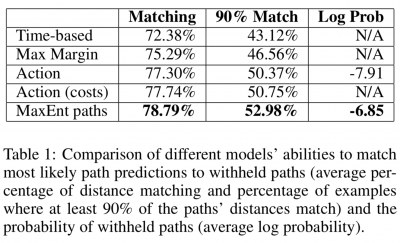
- 경로의 출발지와 도착지를 train set에 학습을 수행한 이후, test set의 경로를 모델링할 수 있는 실험해봤을때 이전 모델들보다 좋은 결과를 보임