05 May 2019

Paper

1. Introduction

Inverse Reinforcement Learning (IRL)은 expert로부터의 trajectory sample로 cost function을 학습하는 방법이다. IRL의 단점은 learner가 어떻게 행동해야하는지에 대해 직접적으로 알려주지 않는다는 것이다. Cost function을 통해 간접적으로 task를 학습하기 때문에 이 방식은 필연적으로 학습이 느릴 수 밖에 없다. 본 연구는 Generative adversarial network를 이용하여 중간의 IRL step을 생략하고 데이터를 통해 policy를 직접적으로 학습하는 방법에 대해 소개한다 (model-free imitation learning).

2. Background

주어진 expert policy \(\pi_E\)에 대해 Inverse Reinforcement Learning 문제는 다음과 같이 정의한다.

\[\max_{c \in \mathcal{C}} \big( \min_{\pi \in \Pi} -H(\pi) + \mathbb{E}_\pi[c(s,a)] \big) - \mathbb{E}_{\pi_E} [c(s, a)],\\ \text{where } H(\pi) \triangleq \mathbb{E}_\pi [ -\log \pi(a|s)] \text{ is the } \gamma \text{- discounted causal entropy of the policy } \pi.\]

또한 cost를 최소화하는 high-entropy policy는 다음과 같이 정의한다.

\[RL(c) = arg\min_{\pi \in \Pi} -H(\pi) + \mathbb{E}_{\pi} [c(s,a)]\]

3. Characterizing the induced optimal policy

IRL은 expert policy가 다른 모든 policy들보다 낮은 cost를 발생하도록 하는 cost function을 찾는 것과도 같다.

\[IRL_{\psi} = arg\max_{c \in \mathbb{R}^{S \times A}} -\psi(c) + \big( \min_{\pi \in \Pi} -H(\pi) + \mathbb{E}_{\pi}[c(s,a)] \big) - \mathbb{E}_{\pi_E}[c(s,a)],\\ \text{where } \psi \text{ is a cost regularizer}.\]

이때 우리가 관심있어하는 것은 RL(\(\tilde{c}\))의 결과로 얻어지는 policy다 (\(\tilde{c}\)은 IRL의 결과). Policy \(\pi\)에 대한 occupancy measure가 \(\rho_\pi : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R} \text{ as } \rho_\pi (s, a) = \pi(a \mid s) \sum_{t=1}^{\infty} \gamma^t P(s_t = s \mid \pi)\)이고, 임의의 cost function \(c\)에 대해 \(\mathbb{E_\pi}[c(s,a)] = \sum_{s,a} \rho_\pi (s, a) c(s,a)\)일때, 이를 RL과 IRL의 합성함수로 나타내보자.

Proposition 3.1

\[RL \circ IRL_\psi (\pi_E) = arg\min_{\pi \in \Pi} -H(\pi) + \psi^* (\rho_\pi - \rho_{\pi_E})\]

Proof

\[\begin{align*} RL \circ IRL_\psi (\pi_E) &= arg\min_{\pi \in \Pi} \: \max_{c \in \mathbb{R}^{S \times A}} - H(\pi) + \mathbb{E}_{\pi}[c(s,a)] - \mathbb{E}_{\pi_E}[c(s,a)] -\psi(c)\\ &= arg\min_{\pi \in \Pi} \: \max_{c \in \mathbb{R}^{S \times A}} - H(\pi) + \sum_{s,a} \rho_\pi (s, a) c(s,a) - \sum_{s,a} \rho_{\pi_E} (s, a) c(s,a) -\psi(c)\\ &= arg\min_{\pi \in \Pi} \: \max_{c \in \mathbb{R}^{S \times A}} - H(\pi) + \sum_{s,a} \big( \rho_\pi (s, a) - \rho_{\pi_E} (s, a) \big) c(s,a) -\psi(c)\\ &= arg\min_{\pi \in \Pi} -H(\pi) + \psi^* (\rho_\pi - \rho_{\pi_E}),\\ &\text{where } \psi^* \text{ is a conjugate function}. \end{align*}\]

• [참고] Conjugate function: \(f^*(x) = \sup_{y \in \mathbb{R}^{S \times A}} x^T y - f(y)\)

다르게 말하면 위 문제는 \(\psi^*\)에 의한 (\(\pi\)와 \(\pi_E\)의) occupancy measure 간의 차이가 최대한 작게끔 하는 것이다.

또한 \(\psi\)가 상수함수라면, 위 문제는 cost \(c(s,a)\)가 inequality constraint에 대한 dual variable인 최적화문제로 정의할 수 있다.

\[\min_{\pi \in \Pi} -H(\pi) \text{ subject to } \rho(s, a) = \rho_E(s,a) \: \forall s \in \mathcal{S}, a \in \mathcal{A}.\]

Lemma 3.1

(Theorem 2 of Syed et al.) 만약 \(\rho \in \mathcal{D}\)이면, \(\rho\)는 \(\pi_\rho (a|s) \triangleq \rho(s, a) / \sum_{a'} \rho(s, a')\)에 대한 occupancy measure이고, \(\pi_\rho\)는 occupancy measure \(\rho\)와 상응하는 유일한 policy다.

Lemma 3.2

\(\tilde{H}(\rho) = - \sum_{s,a} \rho(s, a) \log(\rho(s, a) / \sum_{a'} \rho(s, a')\)라고 하자. \(\tilde{H}(\rho)\)가 모든 \(\pi \in \Pi\)와 \(\rho \in \mathcal{D}\)에 대해 strictly concave면, \(H(\pi) = \tilde{H}(\rho_\pi)\) 그리고 \(\tilde{H}(\rho) = H(\pi_\rho)\)가 성립한다.

Lemma 3.1, 3.2에 의해 위에서 정의한 문제는 또한 아래와 같이 표현할 수 있다.

\[\min_{\rho \in \mathcal{D}} -H(\rho) \text{ subject to } \rho(s, a) = \rho_E(s,a) \: \forall s \in \mathcal{S}, a \in \mathcal{A}.\]

즉, IRL은 occupancy measure가 expert의 것과 일치하는 policy를 얻어내는 과정이라고도 볼 수 있다.

4. Practical occupancy measure matching

3에서 유도한 최적화 문제는 다음의 이유로 그다지 실용적이라고 보기 어렵다.

• 제한된 수의 expert trajectories만이 제공된다.
• 아주 큰 환경에 대해서는 문제가 intractable해진다. 가령, constraint의 갯수가 어마어마하게 많아진다. (See \(\mathcal{S}\), \(\mathcal{A}\))

문제를 large environment에 적합하게 만들기 위해 우선 3에서 유도한 문제를 relax하자.

\[\min_\pi d_\psi (\rho_\pi, \rho_E) - H(\pi)\]

여기서 \(d_\psi (\rho_\pi, \rho_E)\)는 occupancy measure가 다를수록 smoothly penalize시키는 함수다.

Entropy-regularized apprenticeship learning

Apprenticeship Learning via Inverse Reinforcement Learning (이하 APP)에서는 IRL문제를 다음과 같이 정의하였다.

\[\min_\pi \max_{c \in \mathcal{C}} \mathbb{E}_\pi [c(s,a)] - \mathbb{E}_{\pi_E}[c(s,a)]\]

이 문제의 안쪽 max를 변형해보자. \(\begin{align*} \max_{c \in \mathcal{C}} \mathbb{E}_\pi [c(s,a)] - \mathbb{E}_{\pi_E}[c(s,a)] &= \max_{c \in \mathbb{R}^{\mathcal{S} \times \mathcal{A}}} -\delta_{\mathcal{C}}(c) + \sum_{s,a} (\rho_\pi (s,a) - \rho_{\pi_E}(s,a))c(s,a)\\ &= \delta^*_{\mathcal{C}} (\rho_\pi - \rho_{\pi_E}) \end{align*}\) \(d_\psi (\rho_\pi, \rho_E) = \delta^*_{\mathcal{C}} (\rho_\pi - \rho_{\pi_E})\)로 둔다면 relaxed problem은 다음과 같아진다.

\[\min_\pi - H(\pi) + \max_{c \in \mathcal{C}} \mathbb{E}_\pi [c(s,a)] - \mathbb{E}_{\pi_E}[c(s,a)]\]

허나, 위의 고전적인 방법은 basis function \(f_1, ..., f_d\)가 아주 잘 디자인 되어있지 않은한, expert behaviour를 잘 설명하리라 보장할 수 없다. 이 방법을 large state, action space에 대한 policy function approximation과 더 효과적인 regularizer \(\psi\)를 통해 확장해보도록 하자.

5. Generative adversarial imitation learning

좀 더 정확한 occupancy measure matching를 가능하게 하며 large environment에서도 계산적으로 유효한 새로운 cost regularizer를 다음과 같이 정의한다.

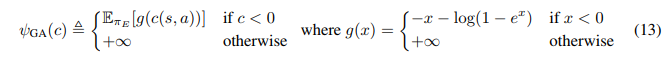
위의 regularizer는 cost function이 expert state-action pair에 대해 낮은 cost를 예측하면 penalty를 적게 발생시키고, 반대의 상황에서는 아주 큰 penalty를 발생시킨다. 또한 모든 expert data에 대해 평균을 취하므로 arbitrary expert datasets에 대한 어느정도의 조정이 가능할 것이다.

여기서 conjugate function \(\psi^∗_{GA}\)는 Jensen-Shannon divergence \(D_{JS}\)의 정의로부터 아래와 같이 정리된다.

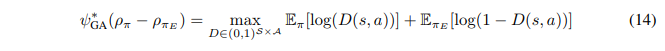
최종적으로 objective function을 정의해보자.

\[\min_\pi \psi^∗_{GA} (\rho_\pi - \rho_{\pi_E}) - \lambda H(\pi) = D_{JS} (\rho_\pi, \rho_{\pi_E}) - \lambda H(\pi),\\ \text{which finds a policy whose occupacy measure minimizes Jensen-Shannon divergence to the expert's.}\]

(아래부터는 RL Korea의 포스팅을 거의 그대로 인용)

다시말해 결국 저자는 smoothly penalizing regularizer를 GAN의 discriminator loss인 Jensen-Shannon divergence 형태로 의도적으로 유도하였으며, 결국 14번 식으로부터 RL-IRL 문제를 Generative adversarial network training problem으로 바꿀 수 있게된 것이다.

GAIL은 IRL과 RL이 병합된 형태이기 때문에, IRL에서 cost function을 업데이트 할때마다 매번 RL에서 optimal policy를 찾는 비용 없이 IRL과 RL을 동시에 학습할 수 있다는 것이 장점이다. 또한 policy와 discrimiator 모두 neural network 를 사용하기 때문에 parameter에 대한 gradient descent 만으로 학습이 가능하다.

주의할 것은 여기서 RL은 model-free policy gradient (PG) 알고리즘으로 학습시키며, PG가 high variance와 small step required 문제를 가지고 있다는 것이다. 이를 해결하고자 저자는 Trust region policy optimization (TRPO) 알고리즘을 사용한다.

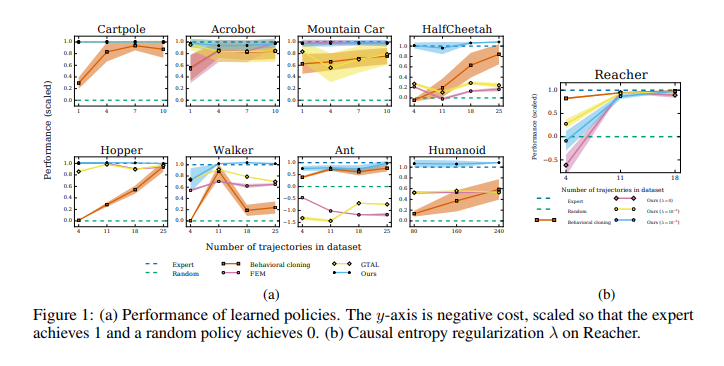
6. Experimental Results

성능 검증을 위해 MuJoCo의 9개의 pysics-based contol task에서 실험을 진행하였다. 또한 각 task마다 GAIL과의 성능 비교를 위한 3개의 baseline을 채택하였다.

• Behaviour cloning: supervised learning 방식으로 policy를 학습
• Feature expectation matching (FEM): \(c(s,a)\)를 basis function의 linear combination set에서 결정
• Game theoretic apprenticeship learning (GTAL): \(c(s,a)\)를 worst case excess cost 사용

---