
1. Introduction
Inverse Reinforcement Learning의 몇 가지 도전과제:
-
a set of demonstrations를 설명할 수 있는 다수의 optimal policies가 존재
-
optimal policy를 설명할 수 있는 다수의 reward functions가 존재
-
continuous, high-dimensional tasks with unknown dynamics에 대해 학습이 어려움
첫 번째 항목의 불확실성(ambiguity)은 Zibart et al. (2008)의 연구(Entropy Maximization)에서 효과적인 대안책이 제시되었다. 또한 세 번째 항목은 Ho & Ermon (2016)의 연구(GAIL)에서 adversarial imitation learning를 통해 효과적으로 다룰 수 있음을 보였다.
허나, 2번은 (특히나 유동적인 dynamics를 가진 환경에서) 여전히 큰 도전과제로 남아있다. 이 문제는 reward function을 직접적으로 학습하지 않는 GAIL에서 치명적인 문제로 작용하는데, demonstration setting에 환경의 변동성이 크게 담겨있는 경우에는 제대로 학습하지 못하는 모습을 보인다.
이 연구에서 제안하는 adversarial inverse reinforcement learning (AIRL)은 adversarial formulation을 통해 reward function과 value function을 동시에 학습하며, 동시에 유동적인 dynamics에서도 불변성의(invariant) reward function을 도출할 수 있도록 한다 (disentangled rewards).
2. Background
본문에 들어가기에 앞서 필요한 선행지식을 살펴보자.
Soft Optimal Policy
Expected entropy-regularised discounted reward를 최대화하는 policy다.
\[\pi^* = arg\max_\pi \mathbb{E}_{\tau \sim \pi} \big[ \sum_{t=0}^T \gamma^t (r(s_t, a_t) + H(\pi(\cdot | s_t))) \big]\]Soft optimal policy는 optimal soft Q-function의 exponential에 비례하는 것으로 알려져있다.
\[\pi^* \propto \exp(Q^*_{soft}(s_t, a_t)),\\ \text{where } Q^*_{soft}(s_t, a_t) = r_t(s, a) + \mathbb{E}_{(s_{t+1},...) \sim \pi} \big[ \sum_{t'=t}^{T} \gamma^{t'} (r(s_{t'}, a_{t}) + H(\pi( \cdot | s_{t'}))) \big]\]Inverse Reinforcement Learning (IRL)
IRL은 다음의 maximum likelihood problem을 푸는 것과 같다.
\[\max_{\theta} \mathbb{E}_{\tau \sim D} [\log p_\theta (\tau)],\\ \text{where } p_\theta(\tau) \propto p(s_0)\prod_{t=0}^T p(s_{t+1} | s_t, a_t) \exp(\gamma^t r_\theta(s_t, a_t))\]Deterministic dynamics인 경우 \(p_\theta\)는 다음과 같이 energy-based model로 간소화된다.
\[p_\theta(\tau) \propto \exp(\sum_{t=0}^T\gamma^t r_\theta(s_t, a_t))\]GAN’s discriminator in a trajectory-centric formulation
\[D_\theta (\tau) = \frac{\exp(f_\theta(\tau))}{\exp(f_\theta(\tau)) + \pi(\tau)},\\ \text{where } f_\theta(\tau) \text{is a learned function, and } \pi(\tau) \text{ is precomputed.}\]3. Adversarial Inverse Reinforcement Learning (AIRL)
2에서 정의한 discriminator in a trajectory-centric formulation는 full trajectory를 사용하는 탓에 single state, action pair를 사용하는 것과 비교해 high variance를 발생시킬 여지가 있다. 실제로 실험을 해보면 학습에서 좋지 않은 성능을 보인다. 그러므로 이를 single state, action에 대한 식으로 변경해보도록 하겠다.
\[D_\theta (s, a) = \frac{\exp(f_\theta(s, a))}{\exp(f_\theta(s, a)) + \pi(a | s)}.\]위의 discriminator가 optimality condition을 만족한다면 이는 학습된 policy \(\pi\)가 demonstrations에 대한 policy \(\pi_E\)와 동일하다는 것이다 (즉, 모든 \(s, a\)에 대해 discriminator는 \(\frac{1}{2}\) 값을 반환). 다르게 말하자면 \(\exp(f_\theta(s,a)) = \pi_E(a \mid s)\) 또는 \(f^*(s, a) = \log \pi_E(a \mid s) = A^*(s, a)\)를 만족한다는 것과 같은 의미다.
\(\log \pi(a \mid s) = A(s, a)\)의 관계가 성립하는 이유는 cs294-112의 lecture-15 (slide, video)에 자세히 설명되어 있다.
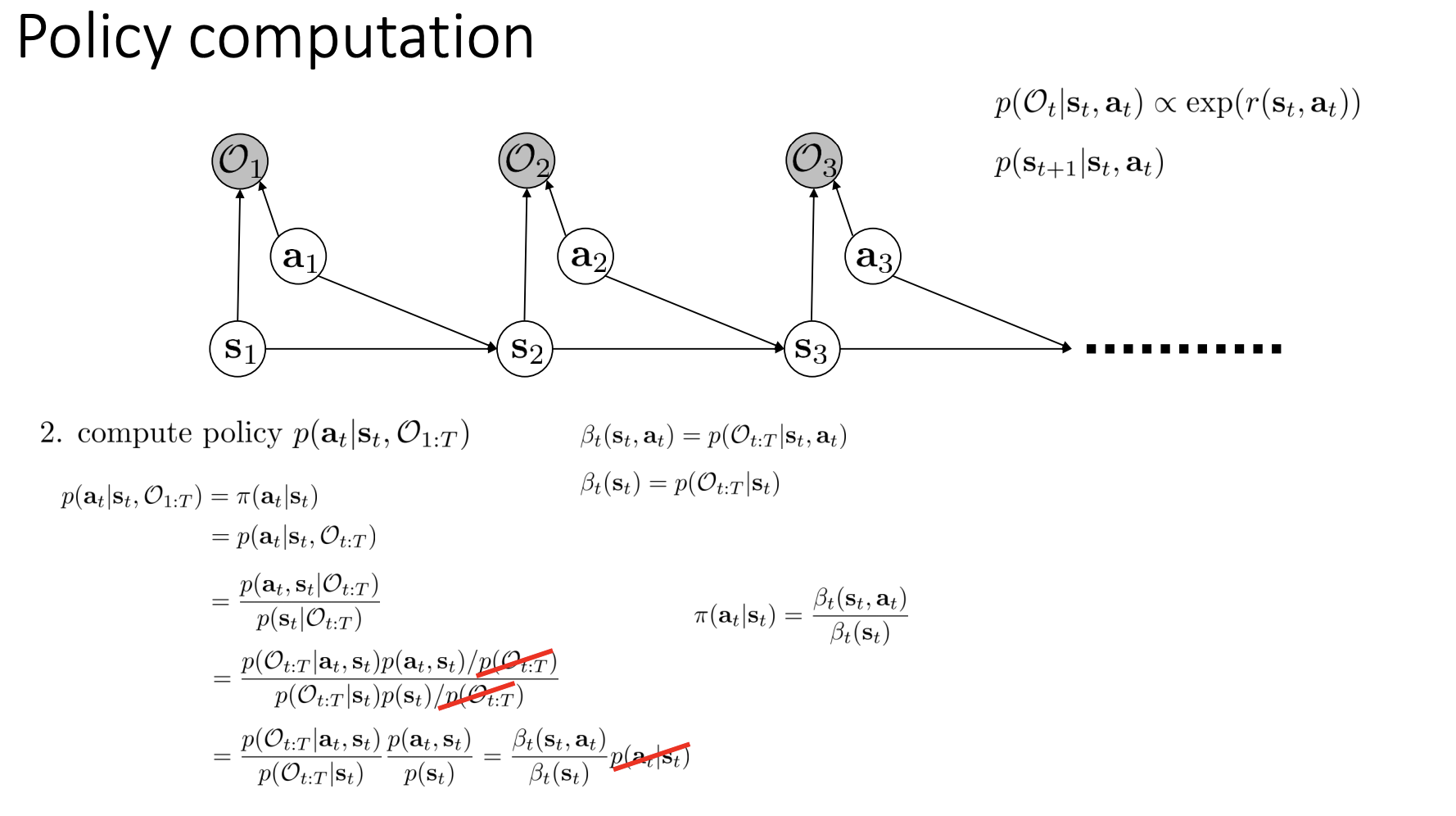

헌데, 문제는 이렇게 얻어진 reward가 ambiguity problem을 갖고있다는 것이다 (heavily entangled reward). 이로인해 environment dynamics가 변하는 경우에도 reward가 안정적으로 잘 동작한다는 보장이 되지 않으며, 실험에서도 environment에 변화가 생길시 agent가 목적된 행동을 제대로 이행하지 못하는 모습을 보인다. 그렇다면 reward Ambiguity Problem이 무엇인지 알아보도록 하자.
4. The Reward Ambiguity Problem
IRL에서 robust reward function을 학습하기가 어려운 이유를 살펴보기에 앞서, optimal policy를 유지해주는 reward shaping formulation에 대해 알아보도록 하자. Ng et al. (1999)에서 reward function에 대한 optimal policy가 결정되었을때, 이 optimal policy를 유지하는 선에서 reward function을 얼마나 변경할 수 있는지 연구한 바가 있다 (policy invariant reward shaping formulation).
자전거가 goal에 도달할 경우 positive reward를 주는 task가 있다고 가정해보자. 추가적으로 최대한 goal에 빨리 도달하게끔 하고 싶다면 아래의 shaping reward function \(F\)를 속도가 높을수록 positive real value를 반환하는 함수로 정의할 수 있을 것이다.
\[R' = R + F, \text{where } R: S \times A \rightarrow \mathbb{R}, F: S \times A \times S \rightarrow \mathbb{R}\]불행하게도 그 결과로 이 자전거는 초기 지점을 빠르게 맴도는 형태의 의도하지 않은 behaviour를 보이게 된다 (Randløv and Alstrøm, 1998). 이것이 강화학습에서 흔히 가장 최종적인 goal에 대해서만 reward를 설정하라고 하는 이유이다.
하지만, 여기서 shaping reward function \(F\)를 다음과 같이 정의한다면 어떨까? (undiscounted case \(\gamma=1\))
\[F(s, a, s') = \Phi(s') - \Phi(s), \text{ where } \Phi \text{ is some function over states}.\]그렇다면 shaping reward function의 총합은 0이 될 것이다.
\[F(s_1, a_1, s_2) + ... + F(s_{n-1}, a_{n-1}, s_n) + F(s_n, a_n, s_1) = 0\]새로운 shaping reward function은 자전거가 시작점을 빙글빙글 도는 문제를 없애줄 것이다. 이러한 역할을 하는 좀 더 일반적인 shaping reward function의 형태를 potential-based shaping function이라 하고, Ng et al. (1999)에서는 이것이 optimal policy invariance에 대한 필요충분 조건임을 증명한다. (자세한 증명 과정은 논문을 참고하자.)

즉, optimal policy invariance를 보장하는 유일한 reward transformation은 다음과 같다.
\[\hat{r}(s,a,s') = r(s,a,s') + \gamma \Phi(s') - \Phi(s),\\ \text{the optimal policy remains unchanged, for any function } \Phi: S \rightarrow \mathbb{R}.\]한가지를 짚고 넘어가자면, 위의 shaped reward function은 dynamics의 변화에 대해서는 robust하지 않을 수 있다. Deterministic dynamics를 \(T(s,a) \rightarrow s'\)로 정의한다면 shaped reward function은 \(\hat{r}(s,a,s') = r(s,a,s') + \gamma \Phi(T(s,a)) - \Phi(s)\)로 볼 수 있는데, 만약에 이때 dynamics가 다른 deterministic dynamics \(T'\)로 교체된다면 새로운 shaped reward function은 \(\hat{r}\)과 동치인 것을 보장할 수 없기 때문이다.
4.1 Disentangled Rewards from Dynamics
\(Q^*_{s,T}(s,a)\)는 reward function \(r\)과 dynamics \(T\)에 대한 optimal Q-function이고, \(\pi^*_{r,T}(a \mid s)\)는 마찬가지로 \(r\)과 \(T\)에 대한 optimal policy라고 하자. Disentangled reward는 다음과 같이 정의한다.
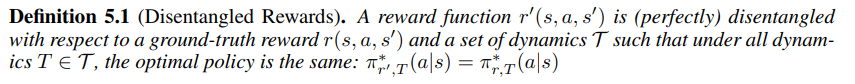
즉, 모든 dynamics \(T\)에 대해 \(r'\)이 ground-truth reward와 동일한 optimal policy를 가진다면 \(r'\)는 (perfectly) disentangled reward인 것이다. (이 논문에서는 sub-optimality까지 내용을 확장하지는 않는다.)
이제 ground-truth reward \(r\)이 state만을 입력으로 하는 함수인 경우에 대해서 고려해보자. 학습된 reward function \(r'\)이 state만을 입력으로 한다면 disentangled reward function의 학습을 보장할 수 있다. 또한 반대의 경우도 마찬가지다. (필요충분조건. 참고로 \(f(s)\)가 state만을 입력으로 하는 함수이므로 \(Q^*_{r', T}(s,a) = Q^*_{r, T}(s,a) - f(s)\)가 성립한다는 것은 곧 두 optimal policies가 동일하다는 것으로도 볼 수 있다.)

Theorem5.1와 5.2에 대한 증명은 논문의 Appendix B & C를 참고하자.
5. Learning Disentangled Rewards With AIRL
3에서 언급했던 discriminator formulation을 다시 살펴보겠다.
\[D_\theta (s, a) = \frac{\exp(f_\theta(s, a))}{\exp(f_\theta(s, a)) + \pi(a | s)}.\]Theorem5.1 & 5.2에 의하면 disentangled reward를 보장하는 조건은 state만을 입력으로 하는 reward function이다. 그러므로 state, action pair를 입력으로 하는 함수 \(f_\theta(s, a)\)는 직접적으로 reward function이 되기에 적합하지 않다. 대신 \(f\)를 state만을 입력으로 하는 reward function과 shaping reward function과의 합으로 나타내보도록 할 것이다.
\[f_{\theta, \phi}(s,a,s') = r_\theta(s) + \gamma \Phi_\phi(s') - \Phi_\phi(s).\]여기에 맞춰 discriminator formulation에도 약간의 변화를 줘보겠다.
\[D_{\theta, \phi} (s, a, s') = \frac{\exp(f_{\theta, \phi}(s, a, s'))}{\exp(f_{\theta, \phi}(s, a, s')) + \pi(a | s)}.\]위 discriminator의 optimality condition에서는 \(f^*(s, a, s') = A^*(s, a) = Q^*(s,a) - V^*(s)\)를 만족할 것이므로 $f$의 shaping reward function은 다음과 같이 유도할 수 있다.
\[\begin{align} f^*(s, a, s') &= A^*(s, a)\\ &= Q^*(s,a) - V^*(s)\\ &= r^*(s) + \gamma V^*(s') - V^*(s) \end{align}\]즉,
\[f_{\theta, \phi}(s, a, s') = r_\theta(s) + \gamma V_\phi(s') - V_\phi(s).\]5.1 The entire training procedure

6. Experiments
실험에서는 다음 두 가지 사항을 중점적으로 검증한다.
- Environment dynamics가 유동적인 상황에서도 AIRL은 robust (disentangled) rewards를 학습할 수 있는가?
- AIRL은 high-dimensional continuous control tasks에서도 잘 동작 하는가?
6.1 Recovering True Rewards In Tabular MDPs

- Figure1: Tabular MDPs에 대해 state만을 입력으로 하는 reward function과 state-action을 입력으로 하는 reward function이 optimal reward를 얼마나 잘 학습하는지 실험.
- Figure2: transfer learning task에서의 learning curve. State만을 입력으로 하는 reward function이 optimal performance를 달성한다.
6.2 Disentangled Rewards in Continuous Control Tasks
High-dimensional environment에서의 domain shift에 대해서 disentangled rewards를 잘 학습하는지 확인하기 위한 실험이다. 실험환경은 training environment와 test environment로 나뉘어진다. Training environment에서 IRL을 통해 rewards를 학습한 뒤, test environment에서도 학습된 reward가 적절한 policy를 도출하는지에 대해 알아본다.
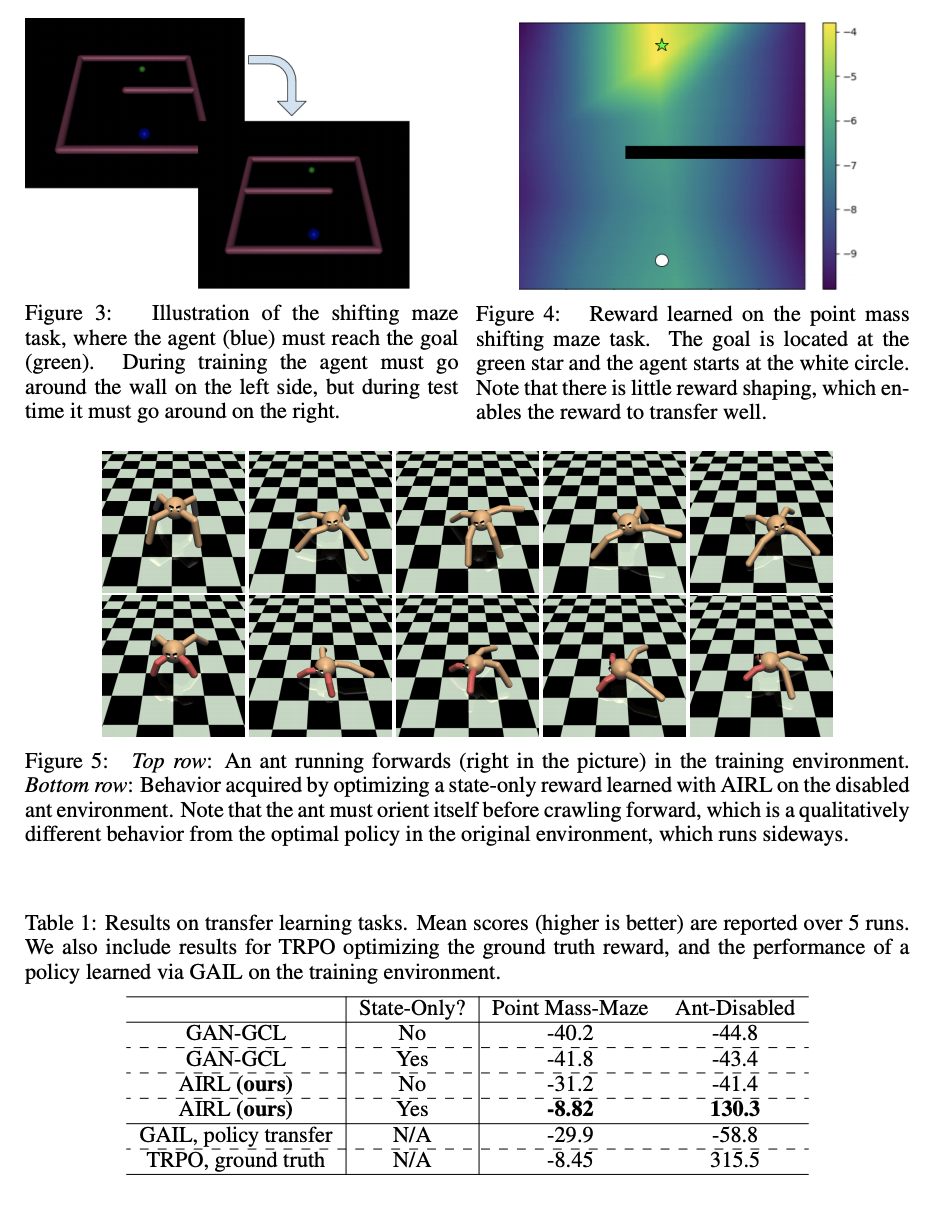
- Fig3: Point Mass-Maze의 training, test environment
- Fig5: 위는 Ant (training environment), 아래는 Ant-Disabled (Test environment)
- Tab1: AIRL만이 Ant-Disabled와 Point Mass-Maze에서 유의미한 결과를 보인다.
6.3 Benchmark Tasks for Imitation Learning
학습된 TRPO에서 얻은 50개의 trajectories를 expert demonstrations라고 가정한다. 이번 실험에서는 test environment를 별도로 분리하지 않으므로 reward transfer에 대해 따로 염두하지 않는다. (state-action reward에 대해서도 실험)
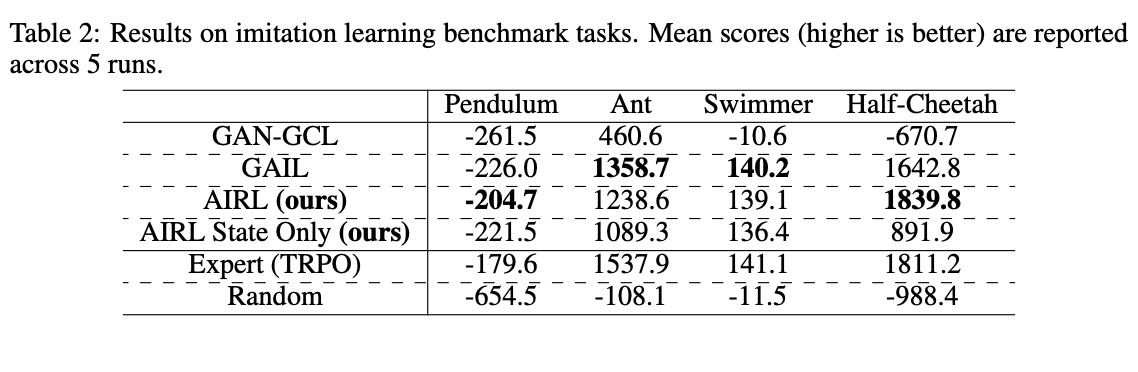
실험에서 AIRL은 generalisation을 요구하지 않는 환경에 대해서도 GAIL에 그다지 뒤지지 않는 성능을 보인다. 이는 Ho & Ermon (2016)의 ‘Direct imitation learning보다 IRL같은 indirect imitation learning의 효율이 떨어진다.’는 주장에 대치되는 결과다.