19 Sep 2018

소개

Probabilistic classification 모델을 학습한다고 가정해보자. 이때 우리의 목표는 모델을 통해 입력에 대한 어떤 확률적 예측(probabilitic prediction)을 하는 것이며, 이 예측이 ground-truth probabilities와 최대한 유사하게끔 모델 파라미터를 조정하는 것이다 [3].

각각의 입력이 둘 중 하나의 class를 가지는 경우로 예를 들어보겠다. 모델은 입력을 가장 잘 묘사하고 있는 class 하나를 골라야 한다. 만약에 ground-truth probabailites가 \(y = (1.0, 0.0)^T\)인데, 모델의 예측(prediction)이 \(\hat{y} = (0.4, 0.6)^T\)이었다면 파라미터는 \(\hat{y}\)가 좀 더 \(y\)에 가까운 값을 갖을 수 있도록 조정되어야 할 것이다.

여기서 ‘가까운’을 판단하는 척도, 다르게 말하자면 \(y\)가 \(\hat{y}\)와 얼마나 다른지 판단하는 방법이 필요하게 된다.

이 포스팅에서는 위의 상황에서 사용될 수 있는 척도인 binary cross entropy가 binary classification task에서 작동하는 원리에 대해 확률적, 정보이론적 관점에서 각각 살펴보도록 하겠다.

Binary Cross Entropy:

$$BCE(x) = -\frac{1}{N} \sum_{i=1}^N y_i \log\big(h(x_i; \theta)\big) + (1-y_i) \log\big(1- h(x_i; \theta)\big).$$

확률 관점의 해석

Likelihood (function) for Bernoulli Distribution

한국어로는 likelihood를 가능도(可能度) 또는 우도(尤度)라고 부른다. 확률함수가 어떤 분포에 대한 관측 데이터의 확률을 나타낸다면, 가능도 함수는 주어진 관측 데이터에 대해 확률 분포의 파라미터가 얼마나 일관되는지를 나타낸다. 참고로 가능도 함수는 확률분포가 아니며, 합하여 1이 되지 않을 수도 있다 [6].

Fig 1. 확률함수와 가능도함수의 차이 (정규분포의 예시) [5]

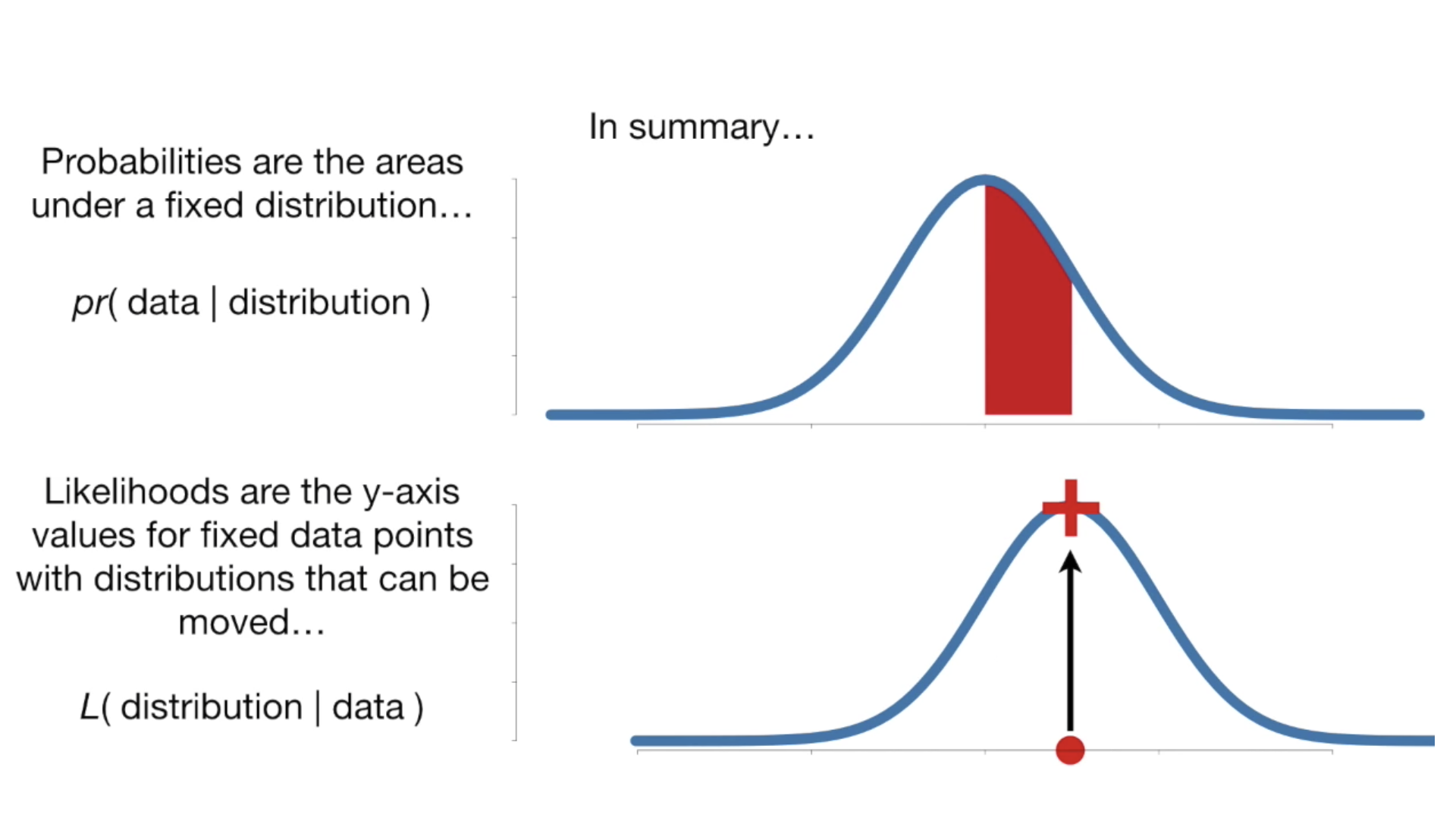
파라미터 \(\pi\) 를 따르는 어떤 확률분포를 \(f(Y; \pi)\) 라고 할때, 관측데이터 \(y\) 에 대한 베르누이분포는 다음과 같다.

$$f(Y = y; \pi) = \pi^y (1-\pi)^{1-y}, \: y \in \{0, 1\}.$$

이 함수는 \(Y=1\)의 입력에 \(\pi\) 를, \(Y=0\)의 입력에는 \({1-\pi}\)를 반환한다.

관측값 \(y\)를 고정시키고 위 함수를 parameter \(\pi\)에 대한 함수로 사용한다면 이는 베르누이분포에 대한 가능도함수가 된다. \(n\)개의 관측데이터에 대해 가능도 함수를 일반화해보자 [1].

$$L(\pi \mid y) = \prod_{i=1}^n f(y_i;\pi), \: y_i \in \{0, 1\}, \: i=1 \dots n.$$

• Note: \(L(\pi \mid y)\)은 조건부확률이 아님을 유의하자.

Loglikelihood (function) for Bernoulli Distribution

Loglikelihood는 likelihood에 \(\log\)함수를 취한 형태로 정의되며 종종 계산적 편의를 위해 likelihood 대신 사용된다. 한 가지 장점을 예로 들면, log를 씌움으로써 확률의 거듭 곱으로 발생할 수 있는 underflow를 방지할 수 있다 [12].

$$l(\pi \mid y) = \log \big( L(\pi \mid y) \big)$$

다음으로는 \(L(\pi \mid y)\)에 대한 loglikelihood를 전개해보자.

$$\begin{align} l(\pi \mid y) &= \log \big(L(\pi \mid y) \big)\\ &= \log \big( \prod_{i=1}^n f(y_i ; \pi) \big)\\ &= \sum_{i=1}^{n} \log \big( f(y_i ; \pi) \big)\\ &= \sum_{i=1}^{n} \log \big( \pi^{y_i} (1-\pi)^{1-y_i} \big)\\ &= \sum_{i=1}^{n} \big( y_i\log (\pi) + (1-y_i) \log(1-\pi) \big)\\ \end{align} $$

\(L(\pi \mid x)\)에 대한 loglikelihood가 바로 negative binary cross entropy의 형태임을 알 수 있다.

Maximum Likelihood Estimation, MLE

주어진 관측데이터에 대해 likelihood function \(L(\pi \mid x)\)를 가장 크게 하는 파라미터 \(\pi\)를 추정하는 것을 maximum-likelihood estimation이라고 한다 [2]. 즉, 관측된 데이터를 기반으로 분포를 추정하는 것이다.

$$ arg \max_{\pi} \: L(\pi \mid y) $$

Likelihood를 최대화하는 \(\pi\) 는 또한 loglikelihood를 최대화하므로, likelihood 대신 loglikelihood를 사용할 수 있다.

$$ arg \max_{\pi} \: l(\pi \mid y) $$

여기서 loglikelihood에 -1을 곱하고 동일한 솔루션을 얻기위해 argmax문제를 argmin문제로 변환한다.

$$ arg \min_{\pi} \: -l(\pi \mid y) $$

위 식을 전개해보자.

$$ arg \min_{\pi} \: -\sum_{i=1}^{n} \big( y_i\log (\pi) + (1-y_i) \log(1-\pi) \big) $$

이로써 binary cross entropy를 최소화하는 문제가 정의되었다. Binary cross entropy는 파라미터 \(\pi\) 를 따르는 베르누이분포와 관측데이터의 분포가 얼마나 다른지를 나타내며, 이를 최소화하는 문제는 관측데이터에 가장 적합한(fitting) 베르누이분포의 파라미터 \(\pi\)를 추정하는 것으로 해석할 수 있다.

정보이론 관점의 해석

Entropy

엔트로피란 확률적으로 발생하는 사건에 대한 정보량의 평균을 의미한다. 정보량은 다음과 같이 정의되며 놀람의 정도를 나타낸다고 볼 수 있다 [9].

정보량:

$$I(X) = \log \big( \frac{1}{p(x)} \big)$$

‘놀람의 정도’란 어떤 의미일까? 예를 들어, 가까운 지인이 길을 걷다가 벼락에 맞았다고 해보자. 벼락에 맞을 확률은 약 1/28만 [8]으로 굉장히 낮은 확률이며, 이 사건이 주변에서 실제로 일어났다면 놀라지 않을 수 없을 것이다. 반면, 동전을 던져서 앞면이 나왔다고 가정해보자. 동전의 앞면이 나올 확률은 대략 1/2이고 빈번히 발생할 수 있는 사건이므로 그다지 대수롭지 않게 여겨질 것이다. 즉, 사건의 발생 확률이 낮을수록 놀람의 정도는 높아지고, 이러한 사건은 높은 정보량을 갖고있는 것으로 여겨진다.

그렇다면 단순히 확률의 역수(\(\frac{1}{p(x)}\))로 정보량을 표현하는 것이 아니라 이에 \(\log\)함수를 취하는 것에는 어떤 의미가 있을까? 바로 \(\log\)함수를 취함으로써 놀람의 정도를 표현하는데 필요한 최소한의 자원을 나타낼 수 있게된다. 가령, 1/8로 발생하는 어떤 사건을 2진수로 표현한다면 밑이 2인 로그함수를 이용하여 (\(-\log_{2} (1/8) = 3\)) 최소 3개의 비트가 필요함을 알 수 있다.

즉, 엔트로피는 정보량에 대한 기댓값이며 동시에 사건을 표현하기 위해 요구되는 평균 자원이라고도 할 수 있다. (참고원문: The entropy provides an absolute limit on the shortest possible average length of a lossless compression encoding of the data produced by a source. [9])

엔트로피:

$$ H_p(X) = \mathbb{E}\big[I(X)\big] = \mathbb{E} \big[ \log (\frac{1}{p(X)}) \big] = -\sum_{i=1}^{n} p(x_i)\log(p(x_i)) $$

엔트로피는 불확실성(uncertainty)과도 같은 개념이다. 예측이 어려울수록 정보의 양은 더 많아지고 엔트로피는 더 커진다 [9].

Cross Entropy

Cross Entropy는 두 개의 확률분포 \(p\)와 \(q\)에 대해 하나의 사건 \(X\)가 갖는 정보량으로 정의된다. 즉, 서로 다른 두 확률분포에 대해 같은 사건이 가지는 정보량을 계산한 것이다. 이는 \(q\)에 대한 정보량을 \(p\)에 대해서 평균낸 것으로 볼 수 있다 [4].

Cross Entropy:

$$ H_{p,q}(X) = - \sum_{i=1}^N p(x_i) \log q(x_i) $$

Cross entropy는 기계학습에서 손실함수(loss function)을 정의하는데 사용되곤 한다. 이때, \(p\)는 true probability로써 true label에 대한 분포를, \(q\)는 현재 예측모델의 추정값에 대한 분포를 나타낸다 [13].

Binary cross entropy는 두 개의 class 중 하나를 예측하는 task에 대한 cross entropy의 special case이다.

Binary Classification Task에서의 Cross Entropy:

$$ \begin{align} H_{p,q}(Y|X) &= - \sum_{i=1}^{N}\sum_{y \in \{0,1\}} p(y_i \mid x_i) \log q (y_i \mid x_i)\\ &= -\sum_{i=1}^{N} \big[ p(y_i=1 \mid x_i) \log q(y_i=1 \mid x_i) + p(y_i=0 \mid x_i) \log q(y_i=0 \mid x_i) \big]\\ &= -\sum_{i=1}^{N} \big[ p(y_i=1 \mid x_i) \log q(y_i=1 \mid x_i) + \{1 - p(y_i=1 \mid x_i)\} \log \{1 - q(y_i=1 \mid x_i)\} \big]\\ &= -\sum_{i=1}^{N} \big[ p(y_i) \log q(y_i) + \{1-p(y_i)\}\log\{1-q(y_i)\}\big]\\ \end{align} $$

Kullback–Leibler (KL) Divergence

KL Divergence를 통해 두 확률분포 \(p\)와 \(q\)가 얼마나 다른지를 측정할 수 있다.

KL Divergence:

\[\begin{align} D_{KL}(p \| q) &= \sum_{i=1}^N p(x_i) (\log p(x_i) - \log q(x_i))\\\ & = \sum_{i=1}^N p(x_i) (\log \frac{p(x_i)}{q(x_i)}) \end{align}\]

KL Divergence는 정보량의 차이에 대한 기댓값이다. 만약 \(q\)가 \(p\)를 근사하는 확률분포라면 KL Divergence는 확률분포의 근사를 통해 얼마나 많은 정보를 잃게 되는지 시사한다 [11].

$$ \begin{align} D_{KL}(p \| q) &= \sum_{i=1}^N p(x_i) (\log p(x_i) - \log q(x_i))\\ &= \mathbb{E} \big[ \log \frac{1}{q(x)} - \log \frac{1}{p(x)} \big]\\ \end{align} $$

Fig 2. 두 정규분포간의 KL divergence [10]

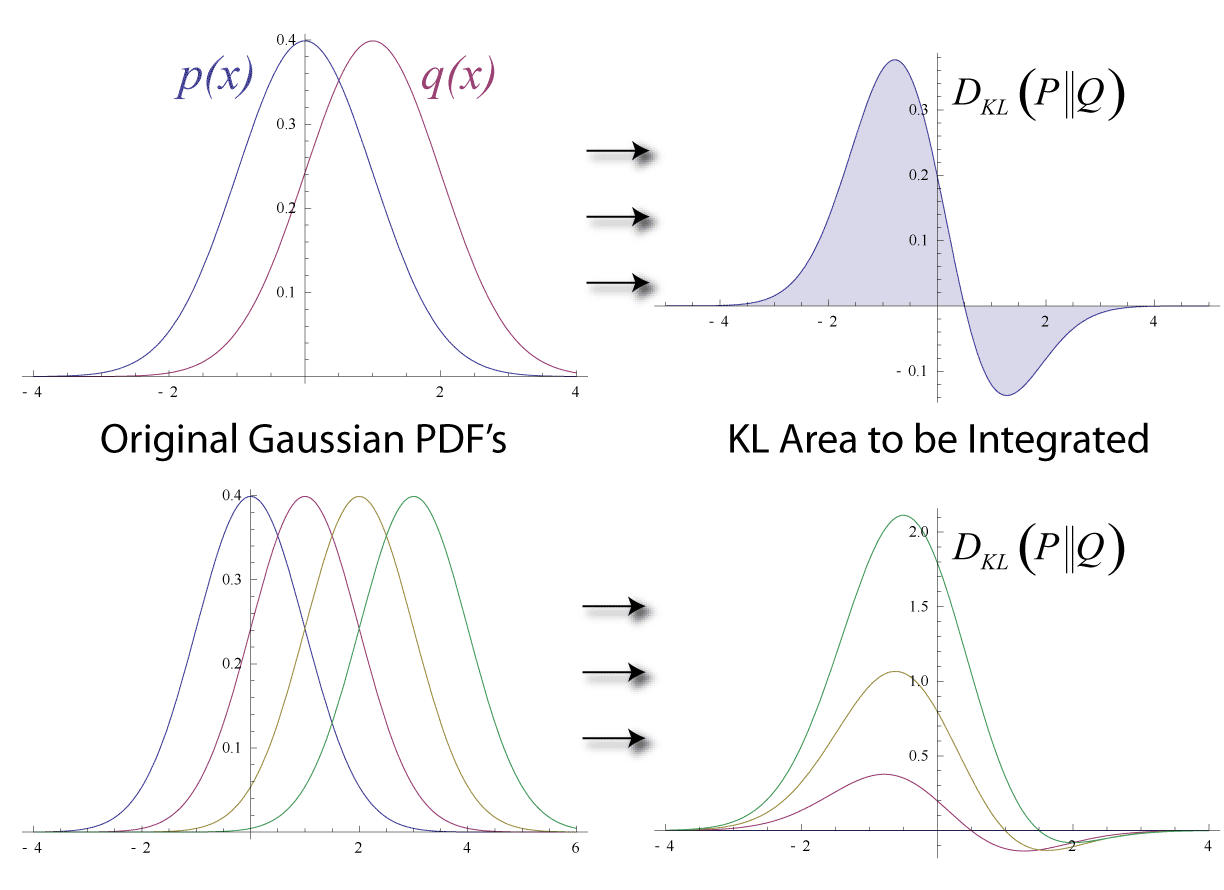
참고로 \(p\)와 \(q\)의 분포가 동일할 경우, 두 정보량의 차는 0이 되므로 이때 KL Divergence는 0을 반환한다.

• Note: KL Divergence는 \(p\)와 \(q\)의 순서가 바뀌면 다른 값을 반환한다. 즉, symmetric하지 않다.

Cross Entropy via KL Divergence

KL Divergence를 변형하면 cross entropy에 대한 식으로 정리된다 [4].

$$ \begin{align} D_{KL}(p \| q) &= \sum_{i=1}^{N} p(x_i)(\log \frac{p(x_i)}{q(x_i)})\\ &= \sum_{i=1}^{N} p(x_i)\log p(x_i) - \sum_{i=1}^{N} p(x_i) \log q(x_i)\\ &= -H_p(X) + H_{p,q}(X) \end{align} $$

이를 \(H_{p,q}(X)\)에 대해 정리하면 다음과 같다.

$$ H_{p,q}(X) = D_{KL}(p \| q) + H_p(X) $$

즉, cross entropy를 최소화하는 것은 KL Divergence를 최소화하는 것과도 같다. 그럼으로써 \(p\)를 근사하는 \(q\)의 확률분포가 최대한 \(p\)와 같아질 수 있도록 예측모델의 파라미터를 조정하게된다.

• Note: 위의 cross entropy에 대한 이야기는 binary classification task에서 뿐만 아니라 더 일반적으로 적용되는 내용이다. (참고원문: Many author use the term “cross-entropy” to identify specifically the negative log-likelihood of a Bernoulli or softmax distribution, but that is a misnomer. Any loss consisting of a negative log-likeligood is a cross-entropy between the empirical distribution defined by the training set and the probability distribution by model. For example, mean squared error is the cross-entropy between the empirical distribution and a Gaussian model [14].)

참고자료

1. Penn State University College of Science. Likelihood & LogLikelihood. [Online]. Available at: https://onlinecourses.science.psu.edu/stat504/node/27/ [Accessed 19 Sep. 2018].

2. Penn State University College of Science. Maximum-likelihood (ML) Estimation. [Online]. Available at: https://onlinecourses.science.psu.edu/stat504/node/28/ [Accessed 19 Sep. 2018].

3. Rob DiPietro. A Friendly Introduction to Cross-Entropy Loss. [Online]. Available at: https://rdipietro.github.io/friendly-intro-to-cross-entropy-loss/ [Accessed 19 Sep. 2018].

4. Donghyun Kwak. Information Theory / Distance Metric for PDF. [Online]. Available at: http://newsight.tistory.com/119 [Accessed 19 Sep. 2018].
5. Josh Starmer. (2018). StatQuest: Probability vs Likelihood. [Video]. Available at: https://youtu.be/pYxNSUDSFH4 [Accessed 19 Sep. 2018].
6. Wikipedia. (2018). 가능도. [Online]. Available at: https://ko.wikipedia.org/wiki/%EA%B0%80%EB%8A%A5%EB%8F%84 [Accessed 19 Sep. 2018].
7. Wikipedia. (2018). Likelihood function. [Online]. Available at: https://en.wikipedia.org/wiki/Likelihood_function [Accessed 19 Sep. 2018].
8. 이왕열. (2009). ‘벼락 맞을 확률’ 생각보다 높다. [Online]. Available at: http://www.sisapress.com/journal/article/126830 [Accessed 19 Sep. 2018].
9. Wikipedia. (2018). Entropy (information theory). [Online]. Available at: https://en.wikipedia.org/wiki/Entropy_(information_theory) [Accessed 19 Sep. 2018].
10. Wikipedia. (2018). Kullback-Leibler divergence. [Online]. Available at: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence [Accessed 19 Sep. 2018].
11. Count Bayesie. (2017). Kullback-Leibler Divergence Explained. [Online]. Available at: https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained [Accessed 19 Sep. 2018].
12. Ian Goodfellow, Yoshua Bengio, and Aaron Courville. (2016). Deep Learning. The MIT Press, p. 128.
13. Wikipedia. (2018). Cross entropy. [Online] Available at: https://en.wikipedia.org/wiki/Cross_entropy [Accessed 19 Sep. 2018].
14. Ian Goodfellow, Yoshua Bengio, and Aaron Courville. (2016). Deep Learning. The MIT Press, p. 129.