Hello Blog!
[요약] High Resolution Face Completion with Multiple Controllable Attributes via Fully End-to-End Progressive Generative Adversarial Networks

Fig1

paper


Problems

  1. 기존의 얼굴 이미지에 대한 image completion 방식들은 저화질의 사진만을 생성해낼 수 있었다.
  2. 기존 대부분의 방법들은 이미지 생성에 있어 유저의 의견이 반영될 수 없었다.
  3. 기존 방식들은 대부분 이미지의 후처리 또는 복잡한 추론과정을 요구했다.


Ideas

  1. U-Net 기반 구조의 fully end-to-end progressive GAN을 이용하여 고화질의 이미지 생성을 해보자. 이때 새롭게 정의된 loss function이 이용될 것이다.
  2. Multiple controllable attributes를 이용하여 생성되는 이미지의 내용을 유저가 조절할 수 있도록 한다.
  3. 이미지 후처리를 요구하지 않으며 단 한번의 forward pass만으로 이미지를 생성한다.


Problem Formulation

\(\Lambda\) 를 이미지 격자(가령, 1024X1024 pixels)라고 하자. 이때 격자 \(\Lambda\) 위에 정의된 RGB이미지를 \(I_\Lambda\) 라고 한다. 이때 \(\Lambda_t\) 와 \(\Lambda_c\) 는 각각 완성시켜야할 target region과 남겨둬야할 context region을 의미하고(\(\Lambda_t \cap \Lambda_c = \emptyset\) and \(\Lambda_t \cup \Lambda_c = \Lambda\) ), \(M_{\Lambda_t}\) 와\(M_{\Lambda_c}\) 는 각 target region, context region에 대한 mask를 의미한다.

Image completion의 목적은 그럴듯한 이미지인 \(I^{\text{syn}}\) 을 생성하는 것이며, 이는 observed image인 \(I^{\text{obs}}\) (\(I^{real}\)로 부터 \(I_{\Lambda_t}^{\text{obs}}\) 의 영역이 제거된 이미지로)부터 생성된다. 또한 generator는 attributes를 조정하여 원하는 방향의 이미지를 생성할 수 있다. 이 attributes는 다음과 같은 N차원의 벡터로 표현하도록 한다. \(A = (a_1, \dotsb , a_N)\) with \(a_i \in \{0, 1\}\). Generator는 다음과 같이 정의될 수 있다.

\[I^{\text{syn}} = G(I^{\text{obs}}, M, A; \theta_G)\]

\(\theta_G\) 는 generator에 대한 모든 파라미터를 의미한다. 여기서 두 context region \(I_{\Lambda_c}^{\text{obs}}\) 와 \(I_{\Lambda_c}^{\text{syn}}\) 는 굉장히 유사하도록 유지되어야 한다.

Generator는 고차원의 거대한 이미지 공간에서 conditional probability model \(P_G(I^{\text{syn}} \mid I^{\text{obs}},M,A)\) 를 아주 근접하게 추정할 수 있도록 학습해야 한다.


The proposed Fully End-to-End Progressive GAN

Fig2

GAN은 다음과 같이 discriminator와 generator 사이의 minmax게임으로 정의된다.

\[min_G max_D L_{adv}(G, D) = E_{z \sim p_{noise}(z)} \big[ 1 - log(1 - D(G(z))) \big] + E_{I \sim p_{data}(I)} \big[ log D(I) \big]\]

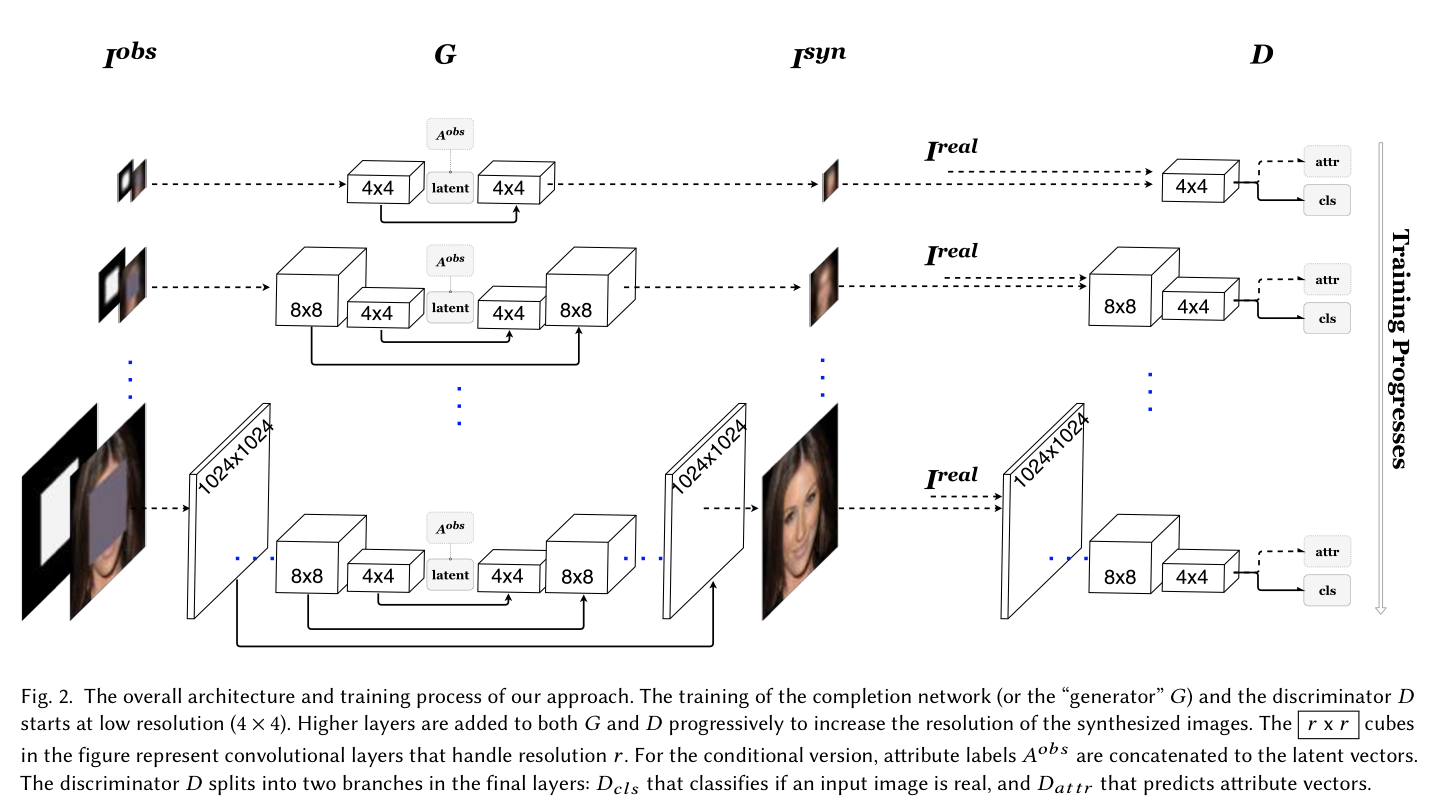
이 논문에서는 binary mask image와 observed image(\(I^{\text{obs}}\))를 encoder에 입력하여 latent vector z를 얻고, latent vector z와 attribute vector를 generator의 입력으로 완전한 이미지를 생성한다.

\[G(I^{obs}, M, A; \theta_G) = G_{compl}(G_{enc}(I^{obs}, M; \theta_G^{enc}), A; \theta_G^{compl})\]

위의 Fig2에서 볼 수 있는 것처럼 여기서의 \(G_{compl}\) 과 \(G_{enc}\) 는 대칭의 형태를 보인다.

Discriminator의 경우, ground truth image 또는 generator에 의해 생성된 이미지가 입력되며 attribute vector와 ground truth 이미지의 판별을 위한 두 개의 output branches를 갖게된다.

\[D(I;\theta_D) = \{ D_{cls}(F(I;\theta_D^F);\theta_D^{cls}), D_{attr}(F(I;\theta_{D}^F); \theta_D^{attr}) \}\]

다음으로는 학습에 대한 더 세부적인 사항들에 대해 살펴보자.


Generating \(I^{obs}\) and \(A^{obs}\)

임의의 mask M을 생성한 뒤에, M을 이용하여 target region을 제거하면 \(I^{obs}\) 를 얻을 수 있다. 우선 mask M을 생성하는 방법에 대해 알아보자.

  1. All-zero one-channel image 위로 어떤 직사각형의 위치와 크기를 임의로 고른다.

  2. low resolution noise(e.g. 4X4, drawn from uniform distribution) image를 생성하고, 이를 앞서 선택된 직사각형의 크기가 되도록 (bi-linear interpolation과 함께) upsampling한다.

위 과정의 결과로 continuous value를 가진 rectangular region을 얻게 되는데, threshold를 이용하여 이를 binary mask로 변환하게되면 mask M을 얻을 수 있다(denote by \(M \sim p_{mask}(M)\)).

한편, Atribute vector \(A^{obs}\) 는 다음과 같은 방법을 통해 생성된다.

\[A^{obs} = \begin{cases} \begin{align} A^{real}, &&\text{if $p < 0.5$.} \\[2ex] (a_1, \dotsb, 1-a_i, a_{i+1}, \dotsb, a_N; \text{for all $j$, $a_j \in A^{real}$}, &&\text{otherwise}. \end{align} \end{cases}\\ \text{where } p \sim U(0,1) \text{ and } i \in [1, N] \text{ is a randomly chosen index. (denote by } A^{obs} \sim p_{attr}(A^{real}))\]


Loss Functions

\[\begin{align} l(I^{real} M, I^{obs}, A^{obs} \mid G, D) &= (1 - log(1 - D_{cls}(I^{syn}))) + logD_{cls}(I^{real}), \\ L_{adv}(G, D) &= E_{I^{real} \sim p_{data}(I), M \sim p_{mask}(M), A^{obs} \sim p_{attr}(A^{real})} \big[ l(I^{real}, M, I^{obs}, A^{obs} \mid G, D) \big]. \end{align}\]


\[\begin{align} L_{attr}(I^{real}, A^{real}, M, I^{obs}, A^{obs} \mid G, D) = &\sum_{i=1}^N (a_i^{real} log (\hat{a_i^{real}}) + (1 - a_i^{real})log(1-\hat{a_i}^{real})) +\\ &\sum_{i=1}^N(a_i^{obs} log(\hat{a_i}^{obs}) + (1-a_i^{obs})log(1 - \hat{a_i^{obs}})). \end{align}\]


\[\begin{align} L_{rec}(I^{real}, M, I^{obs}, A^{obs} \mid G) = &\| \alpha \cdot M \odot (I^{real} - I^{syn}) \|_1 +\\ &\|(1-\alpha) \cdot (1 - M) \odot (I^{real} - I^{syn}) \|_1.\\ \end{align}\\\\ \text{where } \odot \text{represents element-wise multiplication and } \alpha \text{ is the trade-off parameter.}\]


\[L_{feat}(I^{real}, M, I^{obs}, A^{obs} | \phi, G) = \| \phi_j(I^{real}) - \phi_j(I^{syn})\|_2^2\]


\[L_{bdy}(I^{real}, M, I^{obs}, A^{obs} \mid G) = \| w \odot (I^{real} - I^{syn}) \|_1.\]


Total Loss

앞서 정의한 다섯가지의 loss를 각각 trade-off parameter \(\lambda\) 와 곱한뒤 모두 더해주면 최종 Loss가 완성된다.

\[\begin{align} min_G max_D L(G, D) = &L_{adv} (G, D) + \lambda_{attr} \cdot L_{attr}(G, D) +\\ &\lambda_{rec} \cdot L_{rec}(G) + \lambda_{feat} \cdot L_{feat} (G, \phi) + \lambda_{bdy} \cdot L_{bdy}(G). \end{align}\]


Network Architectures

Fig3

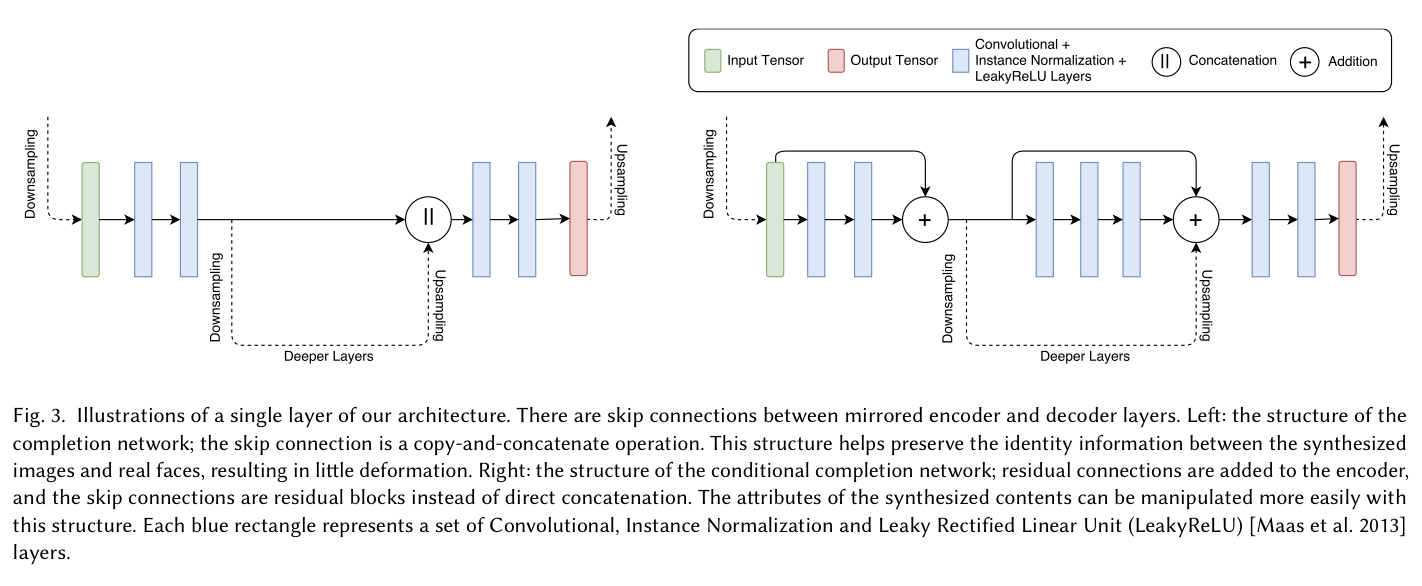
이 모델의 generator \(G\)는 \(G_{enc}\)와 \(G_{compl}\)로 구성되는 U-shape network로 구현된다. \(G_{enc}\)와 \(G_{compl}\)의 layer들 사이에는 U-Net, Hourglass network와 같은 residual connection이 존재하는데, 이는 여러 scale에 대한 정보를 잘 활용하기 위함이다. Fig3는 좌측부터 각각 generator의 학습과정에 attribute vector가 없을때 / 있을때를 나타낸다.


Progressive Training

PGGAN과 거의 동일하다. 아주 낮은 화질(i.e. 4x4)로 이미지 생성을 시작하여, 일정 이상의 interation을 지나고 나면 generator와 discriminator 양 쪽에 동시에 higher resolution layer를 삽입한다. 이때 너무 갑작스러운 변화로 인한 충격을 막기위해 새로 추가되는 layer는 천천히 적용되도록 한다.

1024x1024 보다 낮은 입력 이미지에 대해서는 average pooling을 통해 mask와 real image를 down-sampling한다. 또한 Instance Normalization을 사용하고, 학습의 안정성을 위해 discriminator의 입력으로 최근 생성된 이미지 뿐만 아니라 그 이전에 생성되었던 이미지를 같이 사용한다.(history buffer)


Experiments

Fig4

Fig5

Fig6

Fig7

Fig8


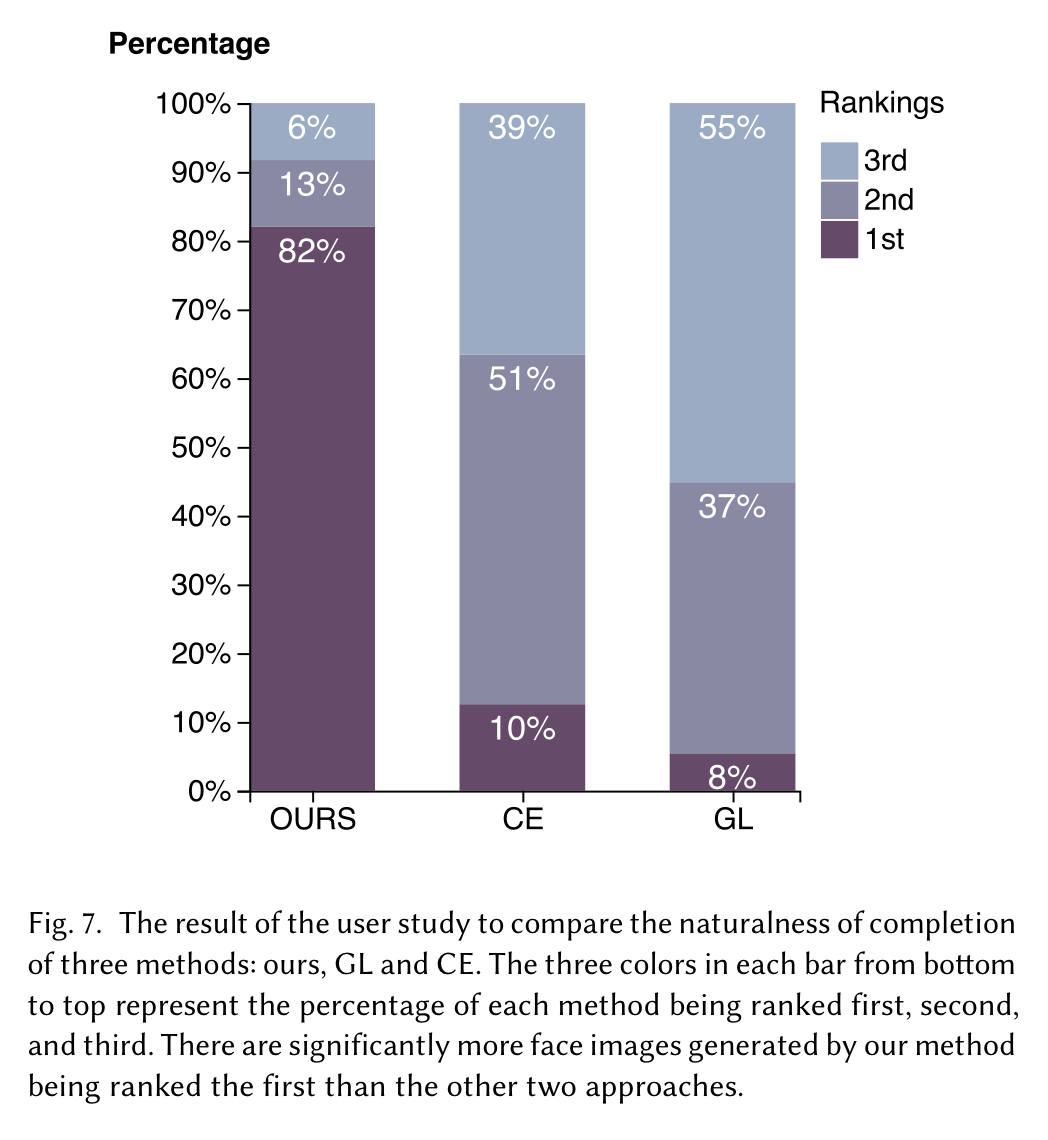
Limitation

Fig9

  1. Inference time은 짧으나 training time이 매우 길다. Titan Xp GPU로 1024x1024 생성모델을 만들기 위해 약 3주 정도의 시간이 걸렸다.
  2. 자세히 들여다보면 고화질의 이미지 생성 모델이 low-level skin texture를 학습하는데에는 실패한 것을 볼 수 있다.
  3. context가 여러가지 세부적인 texture(예를 들어 주근깨)를 갖고있는 경우 이미지가 다소 뿌옇게 생성되었다.
  4. 얼굴에 대한 symmetrical structure를 잡아내지 못했다. (가령, 양 눈의 색깔이 다르게 생성됨.)


Conclusion

목적달성!

© 2017 Kiko. All rights reserved.