Recurrent Neural Network
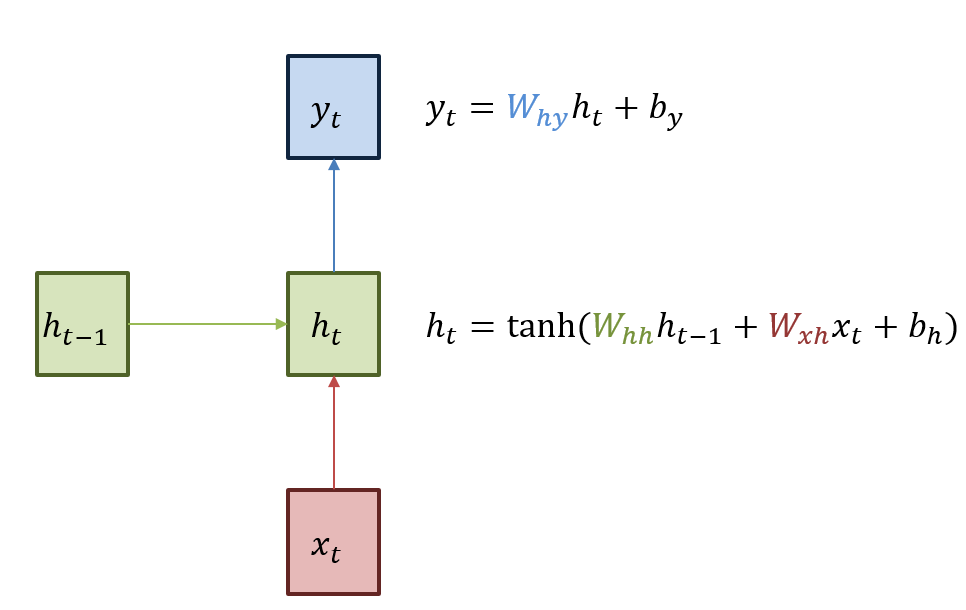 RNN의 \(h_{t}\)에 대한 계산식은 다음과 같다.
RNN의 \(h_{t}\)에 대한 계산식은 다음과 같다.
이때, \(h_{T}\)를 \(h_{t}\)에 대해 미분한다고 하면(T>t), 이는 chain rule에 의해 다음과 같이 표현될 수 있다.
\[\frac{\partial h_{T}}{\partial h_{t}} = \frac{\partial h_{T}}{\partial h_{T-1}} * \frac{\partial h_{T-1}}{\partial h_{T-2}} * ... * \frac{\partial h_{t+1}}{\partial h_{t}}\]여기서,
\(\frac{\partial h_{T}}{\partial h_{T-1}}=W_{hh}*tanh'(W_{hh}h_{T-1} + W_{xh}X_{T} + b_{h})\),
\(\frac{\partial h_{T-1}}{\partial h_{T-2}}=W_{hh}*tanh'(W_{hh}h_{T-2} + W_{xh}X_{T-1} + b_{h})\),
\(...\)
\(\frac{\partial h_{t+1}}{\partial h_{t}}=W_{hh}*tanh'(W_{hh}h_{t} + W_{xh}X_{t+1} + b_{h})\)
이므로
\[\frac{\partial h_{T}}{\partial h_{t}}=W_{hh}^{T-t}*\prod_{i=t}^{T-1}{tanh'(W_{hh}h_{i} + W_{xh}X_{i+1} + b_{h})}\]만약 \(W_{hh}\)의 값이 아주 작다면(-1에서 1사이) 미분식이 깊어질수록(T-t가 커질수록) 결과값은 0에 수렴하게 될 것이다(vanished). 반대로 \(W_{hh}\)의 값이 아주 크다면, 미분식이 깊어질 수록 결과값은 발산하는 형태를 띌 수 있다(exploded).
Long-Short Term Memory
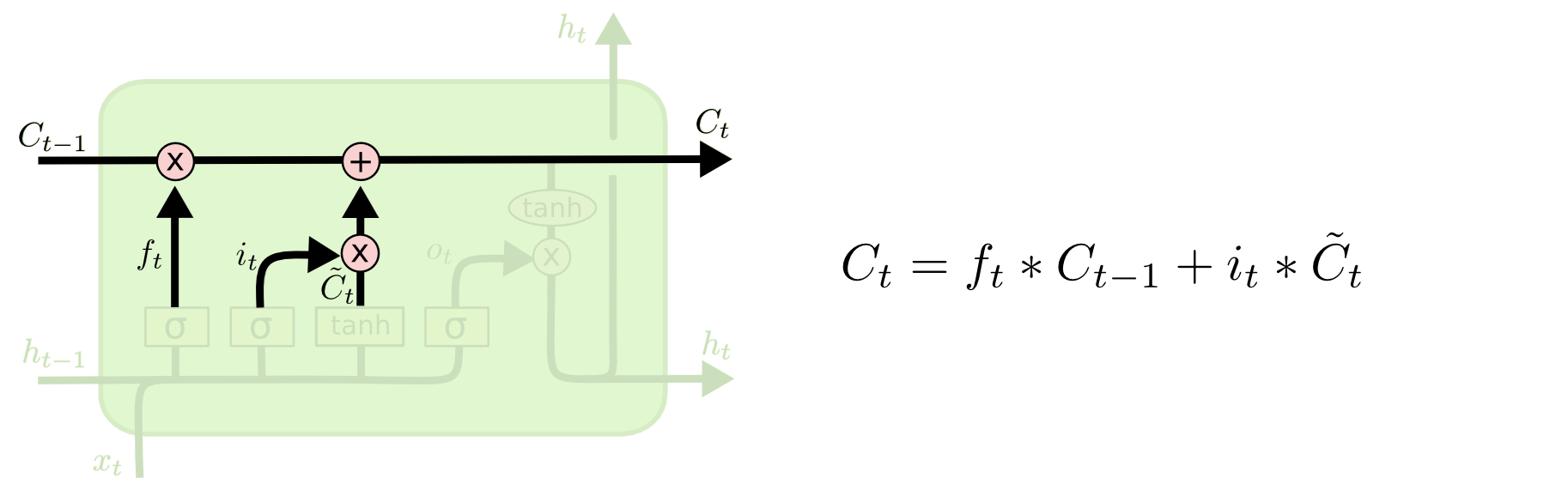
LSTM의 Cell State \(C_{t}\)에 대한 계산식은 다음과 같다.
\[C_{t} = f_{t}*C_{t-1} + i_{t}*\tilde{C_{t}}\]이때, \(C_{T}\)를 \(C_{t}\)에 대해 미분한다고 하면(T>t), 이는 chain rule에 의해 다음과 같이 표현될 수 있다.
\[\frac{\partial C_{T}}{\partial C_{t}} = \frac{\partial C_{T}}{\partial C_{T-1}} * \frac{\partial C_{T-1}}{\partial C_{T-2}} * ... * \frac{\partial C_{t+1}}{\partial C_{t}}\]여기서, \(\frac{\partial C_{T}}{\partial C_{T-1}}=f_{T}, \frac{\partial C_{T-1}}{\partial C_{T-2}}=f_{T-1}, ... , \frac{\partial C_{t+1}}{\partial C_{t}}=f_{t+1}\) 이므로
\[\frac{\partial C_{T}}{\partial C_{t}}=\prod_{i=t+1}^{T}{f_{i}}\]위 식의 \(f\)는 sigmoid함수의 output이기 때문에 (0,1)의 값을 갖게 되는데, 이 값이 1에 가까운 값을 갖게되면 미분값(gradient)이 소멸(vanished)되는 것을 최소한으로 줄일 수 있게된다. \(f\)값이 1에 가깝다는 것은, Cell State 공식에 의하면 오래된 기억(long term memory)에 대해 큰 비중을 둔다는 것과 같은데, 이로인해 gradient 또한 오래 유지된다는 것은 꽤나 흥미로운 현상이다.
+더불어 \(f\)는 1보다 큰 값을 가질 수 없으므로 미분식이 깊어진다고 해서(T-t값이 커진다고 해서) 이로인해 그 값이 넘치게(exploded) 되지는 않는다.
Appendix: Why tanh??
RNN은 vanishing gradient problem에 민감하기 때문에 Gradient를 최대한 오래 유지시킬 수 있는 activation function을 사용하는 것이 바람직하다. 아래 Sigmoid와 Tanh에 대한 그래프를 관찰해보자.
Sigmoid
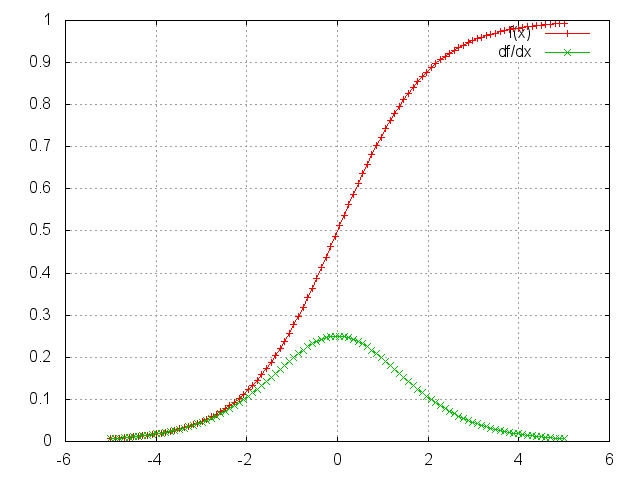
dSigmoid(x)/dx 의 최대값은 0.25 언저리에 불과하다. 즉, 거듭 곱해지게 되면 gradient vanishing이 발생하게 될 것이다.
Tanh
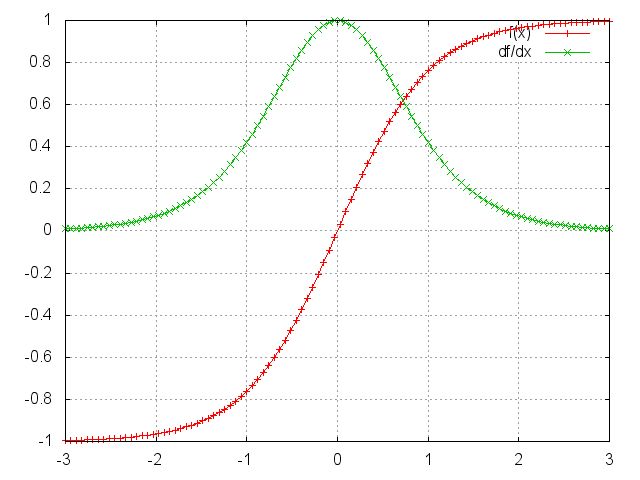
dTanh(x)/dx의 최대값은 1이다. Sigmoid와 비교했을때 gradient vanishing에 강할 것이다.
링크에서 다른 activation function의 그래프도 같이 관찰해본다면 좋을 것 같다.
References
- Quora, “How does LSTM help prevent the vanishing (and exploding) gradient problem in a recurrent neural network?”
- Cross Validated, “How does LSTM prevent the vanishing gradient problem?”
- Quora, “Why do many recurrent NNs use tanh?”
- ReaderDocs-nn, “Transfer Function Layers”
- colah’s blog, “Understanding LSTM Networks”
- ratsgo’s blog, “RNN과 LSTM을 이해해보자!”