Introduction

Big-O notation is used to estimate time or space complexities of algorithms according to their input size. Big-O notation usually only provides an upper bound on the growth rate of the function, so people can expect the guaranteed performance in the worst case. Due to the reason, Big-O is more widely used by developers compared to Big-Theta and Big-Omega.

Definition

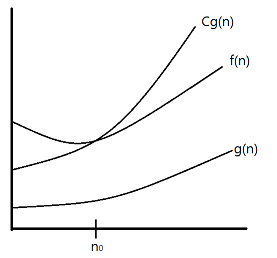Let $f$ and $g$ be two functions defined on some subset of the real numbers. If there is a positive constant $C$ such that for all sufficiently large values of $n$, the absolute value of $f(n)$ is at most $C$ multiplied by the absolute value of $g(n)$. That is, $f(n) = O(g(n))$ if and only if there exists a positive real number $C$ and a real number $n_0$ such that
$|f(n)| \le C|g(n)|$ for all $n \ge n_0.$

Let’s see examples for better understanding. There are two algorithms written in C for sum from 1 to n. (The comment of each line means the operation number.)

// Algorithm1
int calcSum(int n) {
	int i = 1; // 1
	int sum = 0; // 1
	for(; i<=n; ++i)
	{
		sum = sum+i;
	} // 3n+1
	return sum;
}
// Total operation number: 1+1+3n+1 = 3n+3

// Algorithm2
int calcSum(int n) {
	int count = n; // 1
	int sum = 1+n; // 1
	sum = sum*count; // 1
	sum = sum/2; // 1
	return sum;
}
// Total operation number: 1+1+1+1 = 4

Big-O notation for Algorithm1

There exists $C$ and $n_0$ such that $|3n+3| \le C|n|$ for all $n \ge n_0.$ (e.g. $C=4, n_0=3$)
Therefore, $3n+3 = O(n).$

Big-O notation for Algorithm2

There exists $C$ such that $|4| \le C|1|.$ (e.g. $C=4$)
That means, $4 = O(1).$

Polynomial Expression

In real situations, we may face more complicated expressions than the examples above. Let’s suppose that the complexity function $f(n)$ is $n^2+2n+1$, and we need to simplify this expression using Big-O notation. To say the conclusion first, among the three terms $n^2$, $2n$, and $1$, the one with the highest growth rate will be used as follows: $O(n^2)$.

Theorem

$f(n)=O(n^k)$, where $f(n)=a_nn^k+a_{n-1}n^{k-1}+...+a_1n+a_0$ and $a_0,a_1,a_2,...,a_{n-1},a_n$ are real numbers.

Proof:
For all $n \ge 1$,
$|f(n)|=|a_nn^k+a_{n-1}n^{k-1}+...+a_1n+a_0|$ $= |a_n|n^k+|a_{n-1}|n^{k-1}+...+|a_1|n+|a_0|$ $= n^k(|a_n|+|a_{n-1}|/n+...+|a_1|/n^{k-1}+|a_0|/n^k)$
$\le n^k(|a_n|+|a_{n-1}|+...+|a_1|+|a_0|)$
Therefore, $|f(n)| \le Cn^k$ where $C=|a_n|+|a_{n-1}|+...+|a_1|+|a_0|$ and $n_0=1.$ Consequently, $f(n)=O(n^k)$

Going back to $f(n)=n^2+2n+1$, we can use the same approach in order to make Big-O notation for $f(n)=n^2+2n+1$.

For all $n \ge 1,$ ($n_0=1$)
$|f(n)|=n^2+2n+1$
$=n^2(1+2n^{-1}+n^{-2})$
$\le n^2(1+2+1) = 4n^2$
That is, $f(n)=O(n^2)$ ($C=4$, $n_0=1$)

Other Useful Theorems

Many algorithms consist of two or more sub-procedures. We can derive their proper Big-O notations using the sub-procedure’s Big-O.

Theorem 1

Let $f_1(n)=O(g_1(n))$ and $f_2(n)=O(g_2(n))$.
Then, $(f_1+f_2)(n)=O(max(|g_1(n)|,|g_2(n)|))$.

Proof:
By the definition of Big-O, there exists $C_1,C_2,k_1,k_2$ such that $|f_1(n)| \le C_1|g_1(n)|$ for all $n>k_1$ and $|f_2(n)| \le C_2|g_2(n)|$ for all $n>k_2$.
Also, let $n \ge max(k_1,k_2)$, $g(n)=max(|g_1(n)|,|g_2(n)|)$, and $C=C_1+C_2$.
$|f_1(n)+f_2(n)|$
$\le C_1|g_1(n)|+C_2|g_2(n)|$
$\le C_1|g(n)|+C_2|g(n)|$
$= (C_1+C_2)|g(n)|$
$= C|g(n)|$

Corollary:
$(f_1+f_2)(n)=O(g(n))$, where $f_1(n)=O(g(n))$ and $f_2(n)=O(g(n))$.

Theorem 2

Let $f_1(n)=O(g_1(n))$ and $f_2(n)=O(g_2(n))$.
Then, $(f_1 f_2)(n)=O(g_1(n)g_2(n))$.

Proof:
Let $n \ge max(k_1,k_2)$ and $C=C_1C_2$
$|(f_1 f_2)(n)|=|f_1(n)||f_2(n)|$
$\le C_1|g_1(n)|C2|g_2(n)|$
$\le C_1C_2|(g_1g_2)(n)|$
$\le C|g_1g_2|(n)$

References

• Big O notation, Wikipedia, https://en.wikipedia.org/wiki/Big_O_notation
• Discrete Mathematics and its Applications 5th edition, Kenneth H. Rosen, McGraw-Hill Education
• Data Structures for Game Programmers, Ron Penton, PremierPress
• Big-O Notation, openparadigm’s blog, http://openparadigm.tistory.com/20